Questão número 41194

De acordo com o primeiro lema de Kaplansky, a quantidade de subconjuntos de {1, 2, 3,..., n} com p elementos, em que não há números consecutivos, é dada pela fórmula abaixo.

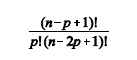
Uma das aplicações desse lema é a contagem do número de maneiras de se sentar 4 meninas e 6 meninos em uma fila de 10 cadeiras, de modo que 2 meninas não fiquem em posições adjacentes. A estratégia para se realizar essa contagem compreende quatro passos. Em primeiro lugar, deve-se contar o número de maneiras de se escolher 4 cadeiras sem que haja cadeiras consecutivas; esse procedimento deve ser feito utilizando-se o lema de Kaplansky. Em seguida, deve-se contar o número de maneiras de organizar as meninas nessas cadeiras. O próximo passo consiste em contar o número de maneiras de se distribuir os meninos nas cadeiras restantes. Por fim, deve-se usar o princípio multiplicativo.

Com base nessas informações, julgue os itens subsecutivos.

A partir dos dados acima, é correto concluir que o número de maneiras de se organizar as 4 meninas nas 4 cadeiras escolhidas é igual a 16.

• C. Certo
• E. Errado