Questão número 534791

Escoamentos a elevados números de Reynolds são caracterizados por terem uma fraca influência dos efeitos viscosos em sua dinâmica. Mesmo nesses tipos de escoamentos, porém, quando um fluido real escoa próximo a uma parede, os efeitos viscosos tornam-se importantes em uma pequena região chamada de cama da limite. Formalmente, a camada limite é definida como sendo a região, de espessura local 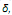  compreendida entre uma parede, na qual o fluido está aderido, e a camada de fluido na qual a velocidade local do escoamento é de 99% da velocidade do escoamento livre Nessa região, para o caso de escoamento bidimensional sem gradiente de pressão, as equações de Navier Stokes podem ser simplificadas se são usadas as seguintes variáveis de similaridade,

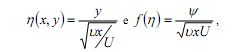
em que 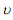 é a viscosidade cinemática do fluido, U é velocidade da corrente livre fora da camada limite,  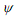 é a função de corrente do escoamento, tal que  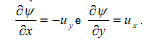Aqui, o vetor velocidade do escoamento é definido como sendo u=(u_x, u_y). Considere um escoamento uniforme com velocidade U sobre uma placa plana de comprimento L e largura 1 m. A tensão de cisalhamento agindo sobre a placa é aproximadamente  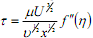 em que µ é a viscosidade dinâmica do fluido e  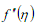 a segunda derivada da função f (n) com relação a (n). O número de Reynolds deste escoamento é definido por  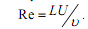A força de arrasto viscoso agindo sobre toda a placa, dividida por µU é dada por:

• A.

  

• B.

  

• C.

  

• D.

  

• E.