Questão número 534794

Suponha que o isolamento térmico de um tubo que transporta um fluido a temperaturas maiores do que a temperatura do meio ambiente deva ser escolhido. Para fundamentar sua escolha, o responsável pelo projeto modelou esse problema como sendo um problema de transferência de calor, em regime permanente, de um tubo cilíndrico de comprimento L , com raio interno r_i e raio externo r_e , no qual escoa um fluido à temperatura constante T_i . A temperatura do ambiente externo é T_e .  A parede do cilindro possui condutividade térmica k constante e não há, no sistema, nenhuma geração interna de calor. Dessa forma, a equação que descreve a distribuição de temperatura na parede do tubo reduz-se a

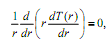
que após integração resulta em T(r) = C₁ln(r)+C ₂, em que as constantes C₁ e C₂ são determinadas com as condições de contorno adequadas ao problema. Com respeito à resistência térmica da parede do tubo, julgue os itens abaixo, marque com F a(s) afirmativa(s) falsa(s) e com V a(s) verdadeira(s) e assinale a opção correta.

( ) Para tubos de mesmo material e raios, aumentando- se o comprimento do tudo em 4 vezes, a resistência condutiva do tubo é reduzida em 4 vezes.

( ) A resistência térmica do tubo é diretamente proporcional à razão de aspecto r_e /r_i.

( ) Sejam dois tubos cilíndricos de mesmo comprimento e feitos do mesmo material, com razões de aspecto r_e /r_i iguais a a e a² . Portanto, a resistência térmica de um dos tubos é duas vezes maior do que a do outro.

• A.

  V,F,V

• B.

  F,V,F

• C.

  V,F,F

• D.

  V,V,F

• E.

  F,V,V