Questão número 550438

Considere que X(t) represente o número de postos de trabalho disponíveis no instante t e que Y(t) represente o número de trabalhadores disponíveis no instante t para a ocupação desses postos. Considere também que X(t) e Y(t) sejam independentes e sigam processos estocásticos de Poisson. Nesse modelo, os valores esperados de X(t) e Y(t) são, respectivamente, iguais a 5t e 6t, em que t é um número real não-negativo, e o excesso de trabalhadores em relação à quantidade de postos disponíveis é definido pela diferença D(t) = Y(t) - X(t). Com base nessas definições, julgue os itens a seguir.

Se X(t) + Y(t) = 100, então Y(t) segue uma distribuição condicional binomial com parâmetros n = 100 e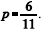

• C. Certo
• E. Errado