Questão número 551355

O enunciado a seguir refere-se às questões de n^os 67 e 68. Avaliações de terrenos baseiam-se, geralmente, em modelos de regressão linear nos quais o preço de venda é uma função de algumas variáveis tais como o tamanho do terreno, suas condições e localização. Uma amostra de terrenos comercializados no último mês coletou dados sobre o preço da venda, em R$ 1 000,00, o tamanho do terreno, em m2, e a distância ao centro da cidade, em km. Primeiramente obteve-se o modelo com apenas a variável tamanho do terreno, X1, como explicativa do preço de venda. Os principais quantitativos relativos a esse modelo foram calculados como:

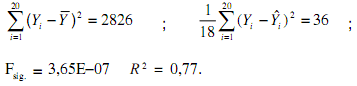
Ao entrar com a variável distância ao centro, o modelo ficou expresso por Yˆ = 9,25 + 2,47 X₁ + 0,78X₂, onde X₁ representa o tamanho do imóvel, em m², e X₂, a distância ao centro, em km. Considerando que todas as variáveis foram testadas e são significativas, analise as afirmações a seguir.

I - Para cada aumento de um metro quadrado no tamanho do terreno, o preço da venda aumenta em 2,47 mil reais, mantendo inalterada a distância ao centro.

II - Para cada aumento de um quilômetro na distância do terreno até o centro, o preço da venda aumenta em 0,78 mil reais, mantendo inalterado o tamanho do terreno.

III - Para um terreno de 40 m², distante do centro 10 km, o preço da venda estimado é de 115,85 mil reais.

É(São) correta(s) a(s) afirmação(ões): (A) I, apenas. (B) II,

• A. I, apenas.
• B. II, apenas.
• C. I e II, apenas.
• D. II e III, apenas.
• E. I, II e III.