Questão número 551919

Suponha que amostras aleatórias simples independentes de tamanhos n1, n2, ..., nk sejam extraídas de k (k 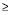2) populações contínuas com o objetivo de testar a hipótese nula de que não há diferenças nos tratamentos, de modo que podemos supor que todas as observações provêm de uma mesma população, contra a hipótese alternativa de que há diferenças na locação dos tratamentos aplicados, ou seja, estamos no contexto da análise da variância de um critério.

Em relação ao teste de Kruskal-Wallis, avalie as afirmativas a seguir:

I - O teste é adequado para situações em que a suposição de normalidade típica da análise de variância não pode ser feita.

II - Para executar o teste, inicialmente as N (N = n₁+ n₂ ... n_k) observações são dispostas como se compusessem uma única amostra e os respectivos postos são determinados. Em seguida são calculadas as somas Ri dos postos das observações de cada amostra i, i= 1, ..., k.

III - A estatística de teste é

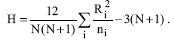
IV %u2013 Assintoticamente, H tem distribuição qui-quadrado com k %u2013 2 graus de liberdade quando a hipótese nula é verdadeira.

Estão corretas somente as afirmativas:

• A. I e II;
• B. III e IV;
• C. I, II e III;
• D. I, III e IV;
• E. II, III e IV.