Questões de Engenharia Mecânica

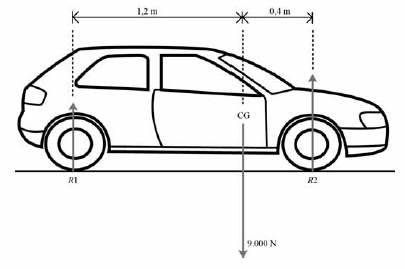
A figura ilustra um automóvel de peso total 9.000 N, parado em um plano horizontal, com o centro de gravidade (CG) localizado a igual distância dos lados direito e esquerdo do automóvel. Nessa situação, as forças de reação, em newtons, em cada pneu dianteiro e em cada pneu traseiro do automóvel são iguais, respectivamente, a

• A. 3.375 e 1.125.
• B. 1.175 e 3.325.
• C. 1.500 e 3.000.
• D. 3.200 e 1.300.
• E. 2.250 e 2.250.

Na formulação do equacionamento do equilíbrio para a solução de problemas da estática de corpos rígidos, a utilização do diagrama de corpo livre exige a determinação do número de reações decompostas nos eixos x, y e z, do sistema de coordenadas cartesianas ortogonais, com base nos tipos de apoio que caracterizam os graus de liberdade. Nesse sentido, o número de reações que os apoios articulado fixo e articulado móvel apresentam nos eixos x, y e z são iguais, respectivamente, a

• A. 2 e 1.
• B. 1 e 0.
• C. 0 e 1.
• D. 1 e 2.
• E. 2 e 3.

Em uma barra sujeita a uma compressão axial no regime elástico linear, as deformações transversais e a deformação axial são, respectivamente,

• A. positivas e negativa.
• B. nulas e positiva.
• C. nulas e negativa.
• D. negativas e positiva.
• E. positivas e positiva.

Assinale a opção correta, a respeito da proporcionalidade entre as tensões e as deformações para o regime elástico (Lei de Hooke), considerando dois materiais (I e II) com as seguintes características: mesmo limite de escoamento para os materiais I e II e módulo de Young do material I igual ao dobro do módulo de Young do material II.

• A. No limite elástico, a deformação do material I é igual ao dobro da deformação do material II.
• B. O módulo de resiliência e a tenacidade são propriedades que independem do módulo de Young do material.
• C. No limite elástico, a deformação do material I é igual à metade da deformação do material II.
• D. A tenacidade do material II é igual ao dobro da tenacidade do material I.
• E. O módulo de resiliência do material I é igual ao dobro do módulo de resiliência do material II.

Uma barra de cobre com 500 mm de comprimento é tracionada por uma tensão de 220 Mpa, causando uma deformação inteiramente elástica, quando o módulo de elasticidade é igual ao quociente da tensão pela deformação. A deformação é expressa pelo quociente da variação do comprimento pelo comprimento inicial. Considerando que o módulo de elasticidade do cobre seja 110 × 10³ Mpa, o alongamento total da barra, em mm, é igual a

• A. 1.
• B. 5.
• C. 10.
• D. 0,01.
• E. 0,5.

Em uma viga isostática submetida à flexão, o momento fletor atuante na seção transversal dessa viga depende do

• A. material construtivo da viga.
• B. momento de inércia de área dessa seção transversal.
• C. módulo de elasticidade do material da viga.
• D. valor da área da seção transversal.
• E. carregamento atuante na viga.

Na situação apresentada, o deslocamento vertical máximo da viga, em cm, é

• A. superior a 0,2 e inferior a 0,6.
• B. superior a 0,6 e inferior a 1,7.
• C. superior a 1,7.
• D. inferior a 0,02.
• E. superior a 0,02 e inferior a 0,2.

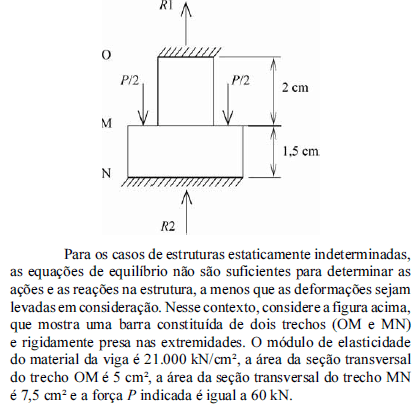
Tendo como referência a figura e as informações apresentadas, e considerando que o sistema esteja em equilíbrio e haja compatibilidade das deformações nos trechos, as reações R1 e R2 são iguais, respectivamente, a

• A. 15 kN e 45 kN.
• B. 50 kN e 10 kN.
• C. 35 kN e 25 kN.
• D. 30 kN e 30 kN.
• E. 20 kN e 40 kN.

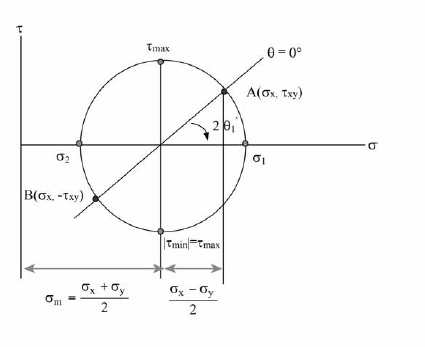
A figura precedente ilustra o círculo de tensões de Mohr, em que a ordenada de um ponto sobre o círculo representa a tensão de cisalhamento (τ) e a abcissa representa a tensão normal (σ). Considerando essa figura, assinale a opção correta.

• A. A maior tensão normal é igual ao raio do círculo.
• B. Uma tensão normal igual a σ_m atua em cada um dos planos de tensões de cisalhamento máxima e mínima.
• C. Se σ_X + σ_Y = 0, então o centro do círculo de Mohr coincide com a origem do plano σ × τ e não se desenvolvem tensões de cisalhamento nesse plano.
• D. Se σ₁ = σ₂, então o centro do círculo de Mohr coincide com a origem do plano σ × τ e verifica-se o estado de cisalhamento puro.
• E. Nos planos σ₁ (maior tensão normal possível) e σ₂ (menor tensão normal possível), o valor das tensões de cisalhamento é, em módulo, igual ao raio do círculo.

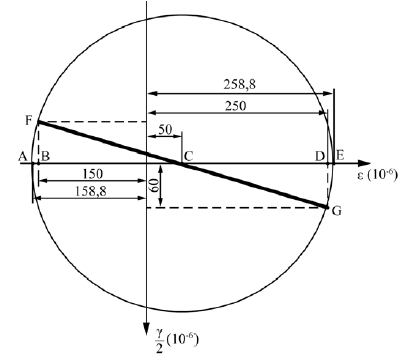
O estado plano de deformações pode ser representado graficamente para se determinar sua solução por meio das componentes das deformações por cisalhamento (γ) e normal (ε). Na situação da figura precedente, que ilustra o círculo de Mohr para um estado plano de deformação, as deformações principais ε_max e ε_min são iguais, respectivamente, a

• A. 258,8 × 10^-6 e 158,8 × 10^-6.
• B. 258,8 × 10^-6 e -158,8 × 10^-6.
• C. -150 × 10^-6 e 60 × 10^-6.
• D. 250 × 10^-6 e -150 × 10^-6.
• E. 250 × 10^-6 e -60 × 10^-6.