Questões de Estatística
Lista completa de Questões de Estatística para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
-
A) 0,135.
B) 0,250.
C) 0,950.
D) 0,861.
Considere o quadro abaixo, representando a distribuição conjunta de X e Y.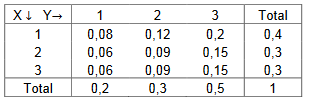
Considere as seguintes afirmações:
I. X e Y são independentes;
II. P(X =1 ou Y=2)=0,14;
III. E(X)=1,9 e E(Y)=2,3.
Pode-se afirmar que
-
A) somente I está correta.
B) I e II estão corretas.
C) I e III estão corretas.
D) Todas as afirmações estão corretas.
I. as distribuições de Bernoulli e Binomial apresentam as mesmas características e, portanto, os mesmos parâmetros;
II. repetições independentes de um ensaio de Bernoulli, com a mesma probabilidade de ocorrência de sucesso, dão origem ao modelo Binomial;
III. o Teorema do Limite Central garante que, para n suficientemente grande, a distribuição de Bernoulli pode ser aproximada pela distribuição de Poisson.
Pode-se afirmar que
-
A) somente II está correta.
B) I e II estão corretas.
C) II e III estão corretas.
D) somente III está correta.
-
A) CV(X) < CV(Y), se k<0.
B) CV(X) = CV(Y), se k<0
C) CV(X) < CV(Y), se K>0.
D) CV(X) > CV(Y), se k>0.
-
A) a e a2.
B) (B) 0 e a2/3
C) a/2 e 2a2.
D) 0 e a2/4.
-
A) normal com média µ = 2 e variância ?2 = 30.
B) qui-quadrado com µ =5 e variância ?2 = 36.
C) normal com média µ = 5 e variância ?2 = 9.
D) normal com média µ = 5 e variância ?2 = 36.
O tempo de permanência de uma plateia num show de 3 horas em um teatro é uma variável aleatória com densidade dada por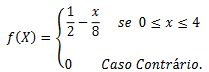
Então, a probabilidade de um expectador, escolhido ao acaso, assistir a mais de 80% do show será aproximadamente de
-
A) 0,12.
B) 0,20.
C) 0,7.
D) 0,16.
Suponha que a variável aleatória bidimensional (X,Y) tenha função densidade de probabilidade (fdp) conjunta:
Então, o valor de mé igual a
-
A) 1/8.
B) 1/5.
C) 8.
D) 1/3.
Considere uma amostra aleatória X1, X2,..., Xn de uma população normal de média µ e variância ?2 = 9 Então, a média e a variância de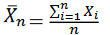 
são, respectivamente,
-
A)
B)
C)
D)
A função densidade de probabilidade (fdp)f de uma variável de aleatória X é dada pela função cujo gráfico é mostrado a seguir.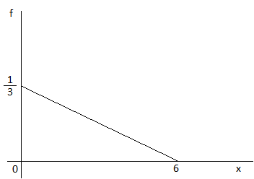
Então, a esperança de X, E(X) é igual a
-
A) 3.
B) 2.
C) 2,1.
D) 1,5.
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
