Questões sobre Inferência estatística
Lista completa de Questões sobre Inferência estatística para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Para avaliar a hipótese nula de que não houve diferença na proporção de pessoas que seguem as orientações entre os dois grupos, foi realizado um teste Z de hipótese bilateral para diferença de proporções ao nível de significância de 5%. Os resultados estão apresentados a seguir.

Com base nos resultados apresentados, assinale a alternativa correta.
-
A) Como o valor p foi maior que o nível de significância, a hipótese nula Ho de igualdade entre as proporções deve ser rejeitada.
B) A probabilidade de rejeitar corretamente a hipótese alternativa Ha é de 20,3%.
C) A proporção de mulheres que não seguiram as orientações foi significantemente menor do que a dos homens.
D) Não houve uma diferença estatisticamente significativa entre as proporções nos dois grupos.
Estatística - Inferência estatística - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
Ao analisar uma amostra aleatória simples composta de 324 elementos, um pesquisador obteve, para os parâmetros média amostral e variância amostral, os valores 175 e 81, respectivamente.
Nesse caso, um intervalo de 95% de confiança de ? é dado por
-
A) (166,18; 183,82).
B) (174,02; 175,98).
C) (174,51; 175,49).
D) (163,35; 186,65).
E) (174,1775; 175,8225).
Estatística - Inferência estatística - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
Texto 7A3-I
O coeficiente de correlação linear de Pearson entre duas variáveis aleatórias discretas X e Y definidas sobre um mesmo espaço amostral é dado por

Uma forma de avaliar a precisão do modelo consiste em comparar o estimador não viesado da variância residual, obtido das diferenças entre os valores observados e os previstos pelo modelo,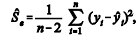 com o estimador não viesado da variância dos valores observados,
com o estimador não viesado da variância dos valores observados, 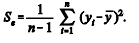
A tabela a seguir apresenta as penas de reclusão (P), em anos, cominadas a um grupo de dez réus, e suas respectivas rendas familiares mensais per capitas (R), em número de salários mínimos, em que a última coluna foi obtida usando a reta ajustada pelo método dos mínimos quadrados.
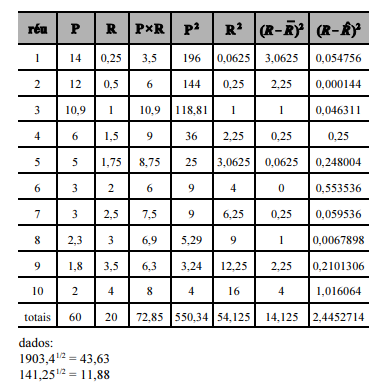
De acordo com o texto 7A3-I, o estimador não viesado 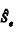 da variância residual é
da variância residual é
-
A) 0,32 < Se < 0,34.
B) 0,30 < Se < 0,32.
C) 0,28 < Se < 0,30.
D) 0,26 < Se < 0,28.
E) 0,24 < Se < 0,26.
Estatística - Inferência estatística - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
Uma fábrica de cerveja artesanal possui uma máquina para envasamento regulada para encher garrafas de 800 mL. Esse mesmo valor é utilizado como média µ, com desvio padrão fixo no valor de 40 mL. Com o objetivo de manter um padrão elevado de qualidade, periodicamente, é retirada da produção uma amostra de 25 garrafas para se verificar se o volume envazado está controlado, ou seja, com média µ = 800 mL. Para os testes, fixa-se o nível de significância ? = 1%, o que dá valores críticos de z de - 2,58 e 2,58.
Com base nessas informações, julgue os seguintes itens.
I É correto indicar como hipótese alternativa H1: µ # 800 mL, pois a máquina poderá estar desregulada para mais ou para menos.II Caso uma amostra apresente média de 778 mL, os técnicos poderão parar a produção para a realização de nova regulagem, pois tal valor está dentro da região crítica para o teste.
III A produção não precisaria ser paralisada caso uma amostra apresentasse média de 815 mL, pois este valor está fora da região crítica para o teste.
Assinale a opção correta.
-
A) Apenas o item I está certo.
B) Apenas o item II está certo.
C) Apenas os itens I e III estão certos.
D) Apenas os itens II e III estão certos.
E) Todos os itens estão certos.
Estatística - Inferência estatística - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
Michael Barrow. Estatística para economia, contabilidade e
administração. São Paulo: Ática, 2007, p. 199 (com adaptações).
João foi julgado culpado pelo crime de assassinato e condenado a cumprir pena de 20 anos de reclusão. Após 10 anos de prisão, André, o verdadeiro culpado pelo delito pelo qual João fora condenado, confessou o ilícito e apresentou provas irrefutáveis de que é o verdadeiro culpado, exclusivamente.
Considerando a situação hipotética apresentada e o fragmento de texto anterior, julgue os itens que se seguem.
I Pode-se considerar que a culpa de João seja uma hipótese alternativa.
II No julgamento, ocorreu um erro conhecido nos testes de hipótese como erro do tipo I.
III Se a hipótese nula fosse admitida pelos jurados como verdadeira e fosse efetivamente João o culpado pelo crime, o erro cometido teria sido o chamado erro do tipo II.
Assinale a opção correta.
-
A) Apenas o item I está certo.
B) Apenas o item II está certo.
C) Apenas os itens I e III estão certos.
D) Apenas os itens II e III estão certos.
E) Todos os itens estão certos.
Estatística - Inferência estatística - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
Para determinado experimento, uma equipe de pesquisadores gerou 20 amostras de tamanho n = 25 de uma distribuição normal, com média µ = 5 e desvio padrão ? = 3. Para cada amostra, foi montado um intervalo de confiança com coeficiente de 0,95 (ou 95%). Com base nessas informações, julgue os itens que se seguem.
I Os intervalos de confiança terão a forma ?i ± 1,176, em que ?i é a média da amostra i.
II Para todos os intervalos de confiança, ?i + 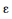
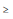 µ
µ 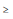 ?i -
?i - 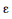 , sendo
, sendo 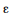 a margem de erro do estimador.
a margem de erro do estimador.
III Se o tamanho da amostra fosse maior, mantendo-se fixos os valores do desvio padrão e do nível de confiança, haveria uma redução da margem de erro 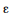 .
.
Assinale a opção correta.
-
A) Apenas o item II está certo.
B) Apenas os itens I e II estão certos.
C) Apenas os itens I e III estão certos.
D) Apenas os itens II e III estão certos
E) Todos os itens estão certos.
Estatística - Inferência estatística - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
-
A)
 0,4410.
0,4410.
B)
 0,3436.
0,3436.
C)
 0,2205.
0,2205.
D)
 0,1125.
0,1125.
E)
 0,1103.
0,1103.
Estatística - Inferência estatística - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
Em uma amostra aleatória de 20 municípios Paraenses, considerando-se os dados da Secretaria de Estado de Segurança Pública e Defesa Social relativos ao crime de lesão corporal, a média é igual a 87 e o desvio padrão igual a 101,9419.
Considerando-se, para 19 graus de liberdade, o coeficiente a = 2,093 e utilizando-se o valor aproximado 4,4721 para a raiz quadrada de 20, com o auxílio da distribuição t, um intervalo de 95% de confiança para a média deverá ter
-
A) limite inferior de, aproximadamente, 38,78.
B) limite superior de, aproximadamente, 143,12.
C) amplitude 2c = 93,45.
D) limite inferior de 39,29 e limite superior de 142,18.
E) limite superior de, aproximadamente, 134,71.
Estatística - Inferência estatística - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2020
A respeito dos intervalos de confiança, julgue os próximos itens.
I Um intervalo de confiança tem mais valor do que uma estimativa pontual única, pois uma estimativa pontual não fornece nenhuma informação sobre o grau de precisão da estimativa.
II Um intervalo de confiança poderá ser reduzido se o nível de confiança for menor e o valor da variância populacional for maior.
III No cálculo de um intervalo de confiança para a média, deve-se utilizar a distribuição t em lugar da distribuição normal quando a variância populacional é desconhecida e o número de observações é inferior a 30.
Assinale a opção correta.
-
A) Apenas o item II está certo.
B) Apenas os itens I e II estão certos.
C) Apenas os itens I e III estão certos.
D) Apenas os itens II e III estão certos.
E) Todos os itens estão certos.
-
A) 400.
B) 1.024.
C) 512.
D) 256.
E) 128.


