Questões sobre Sinos, Assimetrias e Curtoses

Os coeficientes de assimetria e de curtose do valor absoluto são ambos iguais a zero.

• C. Certo
• E. Errado

De uma amostra aleatória simples de 20 trabalhadores da construção civil, foram obtidos os seguintes valores da remuneração mensal, em salários-mínimos:

1, 3, 2, 2, 3, 4, 4, 3, 2, 1, 1, 1, 1, 2, 1, 2, 3, 2, 1, 1.

Considerando essas informações, julgue os próximos itens.

A curtose é uma medida do grau de achatamento da distribuição, sendo definida em função do quarto momento central.

• C. Certo
• E. Errado

Marque V ou F conforme sejam verdadeiras ou falsas as afirmativas. Quando os dados apresentam uma distribuição assimétrica à direita:

( ) a mediana é maior que a média.

( ) a distribuição é unimodal.

( ) a cauda à esquerda é menor que a cauda à direita.

( ) o desvio-padrão é menor que a variância.

( ) a maioria das observações são menores que a média.

A seqüência CORRETA, de cima para baixo, é:

• A. V F V F F
• B. V F V F V
• C. F V F V F
• D. F F V F V

A tabela abaixo mostra, em porcentagens, a distribuição relativa da população brasileira por grupos etários, de acordo com dados dos censos demográficos de 1940 a 2000.

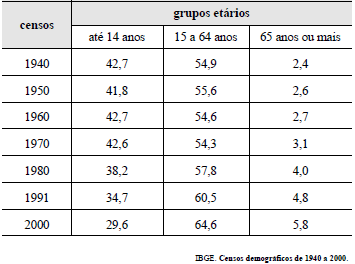
Infere-se dos dados da tabela que, de 1940 a 1970, a população brasileira apresentava-se distribuída uniformemente em relação aos três grupos etários.

• C. Certo
• E. Errado

A distribuição de freqüências de um conjunto de dados apresentou um momento de terceira ordem centrado em relação à média amostral m₃ = -8 e um momento de segunda ordem centrado em relação à média amostral m₂ = 4. O valor do coeficiente m₃ / m₂ ^3/2 permite concluir que essa distribuição de freqüências:

• A.

  é leptocúrtica.

• B.

  é platicúrtica.

• C.

  possui assimetria positiva.

• D.

  possui assimetria negativa.

• E.

  é mesocúrtica.

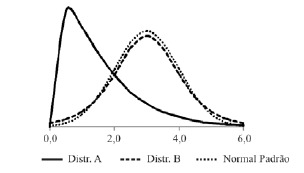
Considerando as densidades de probabilidade ilustradas na figura acima, julgue os itens que se seguem a respeito dos momentos dessas distribuições.

Se a distribuição de B não for normal, então sua curtose é negativa.

• C. Certo
• E. Errado

Um indicador W que mede a qualidade de determinado produto é uma variável aleatória contínua simetricamente distribuída em torno de 7. Tal indicador assume apenas valores positivos e em 75% dos casos seu valor é superior a 3. Com base nessas informações, julgue os itens subseqüentes.

A curtose de W é igual a zero.

• C. Certo
• E. Errado

Em uma agência bancária, 5 empregados foram avaliados pelos empregados supervisores A e B. Os supervisores, após avaliarem o desempenho de cada empregado, atribuiu uma nota de zero a dez. A tabela abaixo mostra o resultado dessa avaliação.

 Com base nessas informações, julgue os próximos itens.

O coeficiente de assimetria de Pearson para as notas dadas pelo supervisor B é positivo, enquanto que o mesmo coeficiente para as notas dadas pelo supervisor A é nulo.

• C. Certo
• E. Errado

Considere que X 1 , X 2 , ..., X 100 seja uma amostra aleatória simples de 100 erros de arredondamento. Cada erro de arredondamento é uma variável aleatória contínua uniformemente distribuída no intervalo  . A soma dos elementos dessa amostra é Y = X 1 + X 2 + ... + X 100 , e  é a média amostral. Com base nessas informações, julgue os itens seguintes.

A curtose da soma Y é positiva.

• C. Certo
• E. Errado

Considere as estatísticas a seguir, em que Y₁, Y₂, ..., Y_n seja uma amostra aleatória simples de uma população com média zero e com momentos centrais finitos.

Q2 = mediana(Y₁, Y₂, ..., Y_n);

A quantidade de estatísticas entre as apresentadas acima, que medem o grau de assimetria é igual a

• A. 0
• B. 1
• C. 2
• D. 3