Questões de Estatística da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

Um analista deseja inspecionar um lote de 500 pacotes com encomendas internacionais. Como essa inspeção requer a abertura de cada pacote, ele decidiu fazê-la por amostragem, selecionando n pacotes desse lote. O analista dispõe de um cadastro que permite localizar precisamente cada pacote do lote por meio de um código de identificação.

Com base nessas informações e nos conceitos de amostragem, julgue os itens a seguir.

Para se calcular o tamanho da amostra com o objetivo de se estimar a proporção de pacotes que necessitam de recolhimento de impostos, independentemente do nível de confiança desejado, o analista deverá usar a fórmula n = 1/E², em que E é o erro amostral.

• C. Certo
• E. Errado

Os exemplos de métodos que permitem estimar as componentes T e S da série temporal z incluem as médias móveis, a suavização exponencial e a regressão.

• C. Certo
• E. Errado

Com relação aos testes de hipóteses paramétricos, julgue os itens subsecutivos.

Define-se poder do teste como a probabilidade de a hipótese nula ser rejeitada quando esta é, de fato, falsa. Logo, o poder do teste é igual a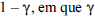  é a probabilidade de haver o erro do tipo I.

• C. Certo
• E. Errado

Um analista deseja inspecionar um lote de 500 pacotes com encomendas internacionais. Como essa inspeção requer a abertura de cada pacote, ele decidiu fazê-la por amostragem, selecionando n pacotes desse lote. O analista dispõe de um cadastro que permite localizar precisamente cada pacote do lote por meio de um código de identificação.

Com base nessas informações e nos conceitos de amostragem, julgue os itens a seguir.

Se n = 50 pacotes selecionados aleatoriamente, então o fator de correção para populações finitas será superior a 0,85.

• C. Certo
• E. Errado

A série temporal xt é estacionária para qualquer valor de .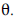

• C. Certo
• E. Errado

Com relação aos testes de hipóteses paramétricos, julgue os itens subsecutivos.

Considere que duas amostras independentes, de tamanhos n₁ > 1 e n₂ > 1, em que n₁ + n₂ < 30, foram retiradas de duas populações normais com variâncias desconhecidas e diferentes. Nessa situação, é correto afirmar que a estatística do teste dada pela diferença padronizada das médias aritméticas dessas duas amostras segue, sob a hipótese nula, distribuição t de Student com n₁ + n₂ – 2 graus de liberdade.

• C. Certo
• E. Errado

Um analista deseja inspecionar um lote de 500 pacotes com encomendas internacionais. Como essa inspeção requer a abertura de cada pacote, ele decidiu fazê-la por amostragem, selecionando n pacotes desse lote. O analista dispõe de um cadastro que permite localizar precisamente cada pacote do lote por meio de um código de identificação.

Com base nessas informações e nos conceitos de amostragem, julgue os itens a seguir.

Considere que o lote de pacotes seja dividido em dois estratos segundo a massa de cada pacote: o primeiro, formado por 400 pacotes que possuem massas inferiores a 1 kg, e o segundo, por 100 pacotes com massas superiores a 1 kg. Nessa situação, se o analista efetuar uma amostragem estratificada de tamanho n = 50 com alocação uniforme, então essa amostra deverá contemplar 40 pacotes do primeiro estrato e 10 pacotes do segundo.

• C. Certo
• E. Errado

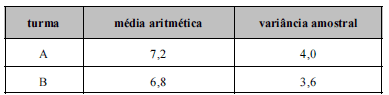
Um estudo foi realizado em determinada escola para se avaliar o efeito, no desempenho dos estudantes, do uso de computadores em sala de aula. Para esse estudo, foram selecionados aleatoriamente 60 alunos de determinado ano escolar, separando-os em duas turmas A e B, cada uma com 30 alunos. Ao longo de um semestre letivo, um método de ensino com auxílio de computadores foi aplicado na turma A, enquanto, nesse mesmo período, outro método sem auxílio de computadores foi aplicado na turma B. Ao final desse semestre, o mesmo teste foi aplicado para os 60 alunos participantes desse estudo. O quadro acima mostra algumas estatísticas acerca das notas obtidas pelos alunos de ambas as turmas.

Considerando essas informações, acerca de probabilidade, inferência e amostragem, julgue os itens a seguir.

Considere que 600 estudantes tenham cursado o ano escolar pertinente a esse estudo na ocasião da sua realização. Nessa situação, a probabilidade de seleção da amostra para o estudo foi inferior a 0,15 e superior a 0,05.

• C. Certo
• E. Errado

Um analista deseja inspecionar um lote de 500 pacotes com encomendas internacionais. Como essa inspeção requer a abertura de cada pacote, ele decidiu fazê-la por amostragem, selecionando n pacotes desse lote. O analista dispõe de um cadastro que permite localizar precisamente cada pacote do lote por meio de um código de identificação.

Com base nessas informações e nos conceitos de amostragem, julgue os itens a seguir.

Na estimação de uma proporção p por amostragem aleatória simples, a variância do estimador é máxima quando p = 0,5.

• C. Certo
• E. Errado

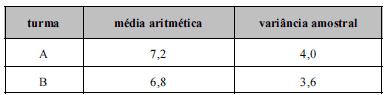
Um estudo foi realizado em determinada escola para se avaliar o efeito, no desempenho dos estudantes, do uso de computadores em sala de aula. Para esse estudo, foram selecionados aleatoriamente 60 alunos de determinado ano escolar, separando-os em duas turmas A e B, cada uma com 30 alunos. Ao longo de um semestre letivo, um método de ensino com auxílio de computadores foi aplicado na turma A, enquanto, nesse mesmo período, outro método sem auxílio de computadores foi aplicado na turma B. Ao final desse semestre, o mesmo teste foi aplicado para os 60 alunos participantes desse estudo. O quadro acima mostra algumas estatísticas acerca das notas obtidas pelos alunos de ambas as turmas.

Considerando essas informações, acerca de probabilidade, inferência e amostragem, julgue os itens a seguir.

• C. Certo
• E. Errado