Questões de Física do ano 2008

Julgue os itens de 81 a 85, com relação a estática.

Considerando a viga apresentada na figura abaixo, os valores dos momentos fletores nos pontos A, B e C são, respectivamente, iguais a: M A = 6 tf m (comprimindo as fibras superiores), M C = 1,0 tf m (tracionando as fibras inferiores) e M B = 1,0 tf m (comprimindo as fibras inferiores).

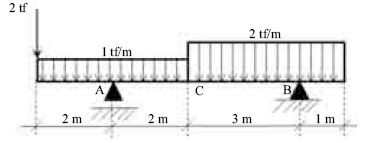
• C. Certo
• E. Errado

Julgue os itens de 81 a 85, com relação a estática.

Para uma estrutura plana, o esforço cortante em uma seção é a soma algébrica das componentes na direção normal à seção, das forças situadas de um dos lados desta seção.

• C. Certo
• E. Errado

Julgue os itens de 81 a 85, com relação a estática.

Os diagramas de esforços são a representação gráfica dos esforços internos atuantes em uma estrutura. Para uma estrutura plana, carregada no mesmo plano, têm-se os diagramas de esforços normais, de esforços cortantes e de momentos fletores e torsores.

• C. Certo
• E. Errado

Julgue os itens subsequëntes, com relação a geometria das massas.

As coordenadas (x, y) do centro de gravidade de uma região plana limitada são dadas pelo quociente entre os momentos estáticos dessa região e a área total da região.

• C. Certo
• E. Errado

Julgue os itens subsequëntes, com relação a geometria das massas.

O momento de inércia polar em relação a um ponto O é igual ao quadrado do momento de inércia em relação a esse ponto, o qual deverá estar na origem do sistema de referência.

• C. Certo
• E. Errado

Julgue os itens subsequëntes, com relação a geometria das massas.

O teorema de Steiner permite a determinação do momento de inércia de uma área por meio da integral do quadrado da distância r de um elemento de área dA até um ponto O escolhido arbitrariamente no sistema de referência.

• C. Certo
• E. Errado

Julgue os itens subsequëntes, com relação a geometria das massas.

Os momentos de inércia, assim como o produto de inércia são grandezas essencialmente positivas.

• C. Certo
• E. Errado

Julgue os itens subsequëntes, com relação a geometria das massas.

A ordenada y do centro de gravidade C do trapézio de bases b e a e altura h, ilustrado na figura abaixo, é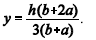

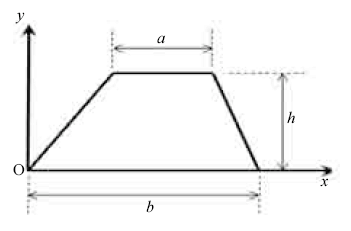
• C. Certo
• E. Errado

Se um corpo rígido encontra-se em translação, então todos os pontos do corpo têm, em qualquer instante, a mesma velocidade e a mesma aceleração.

• C. Certo
• E. Errado

Considere o movimento plano de uma placa metálica qualquer. Nesse caso, se a velocidade linear de um ponto A da placa for conhecida, então as velocidades lineares dos pontos B e C da placa podem ser determinadas a partir da aceleração angular do corpo e dos vetores posição AB e AC.

• C. Certo
• E. Errado