Questões de Matemática do ano 2012

Um bombeiro hidráulico, para fazer a manutenção de umencanamento da cozinha de uma escola, precisou quebrar o piso e uma parede, ambos retangulares e totalmente azulejados.Opiso tinha 4mde largura por 5mde comprimento e a parede tinha 5mde base por 3mde altura. O custo para o reparo e azulejamento é de R$ 20,00 cada metro quadrado. O valor que a escola pagou pelo serviço de reparo e azulejamento foi:

• A.

  R$ 350,00

• B.

  R$ 700,00

• C.

  R$ 850,00

• D.

  R$ 900,00

• E.

  R$ 950,00

Considere as afirmações sobre quadriláteros:

I. Todo paralelogramo tem as diagonais congruentes.

II. As diagonais de um trapézio isósceles são perpendiculares entre si.

III. Todo retângulo possui quatro ângulos internos congruentes.

Então:

• A.

  I e II são verdadeiras, apenas.

• B.

  I, II e III são verdadeiras.

• C.

  II e III são falsas, apenas.

• D.

  I e II são falsas, apenas.

• E.

  e III são falsas, apenas.

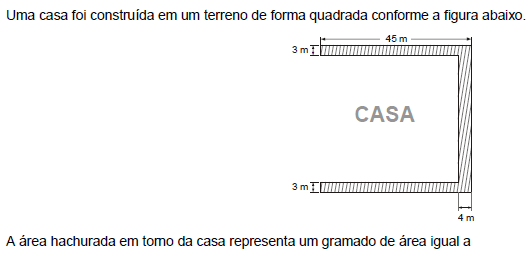
• A.

  535 m².

• B.

  426 m².

• C.

  356 m².

• D.

  225 m².

Uma empresa fabrica enfeites de Natal com a forma de esfera, todos de mesmo tamanho. Eles são acondicionados em embalagens cúbicas, que comportam oito enfeites. Nessas embalagens, cada enfeite fica encostado em outros três, além de tocar duas paredes e a tampa ou o fundo da embalagem. Se as embalagens forem reduzidas, mantendo a forma de cubo, de modo que cada aresta passe a medir metade do comprimento original, cada embalagem passará a comportar, no máximo,

• A.

  um único enfeite.

• B.

  dois enfeites.

• C.

  três enfeites.

• D.

  quatro enfeites.

• E.

  seis enfeites.

• A.

  9x² + 21x

• B.

  12x² + 31x + 20

• C.

  3x² + 10x + 20

• D.

  9x² + 31x

Se um trapézio possui bases medindo 5 cm e 10 cm e lados oblíquos medindo 3 cm e 4 cm, então a sua altura mede:

• A.

  1,2 cm.

• B.

  1,8 cm.

• C.

  2,4 cm.

• D.

  3,2 cm.

Sabe-se que uma pirâmide de base quadrada possui uma área lateral de 9  cm². Se o comprimento da altura dessa pirâmide coincide com o comprimento do lado do quadrado de sua base, então a altura da pirâmide mede:

• A.

  2 cm.

• B.

  2  cm.

• C.

  3 cm.

• D.

  3  cm.

Se o comprimento da diagonal de um cubo é 6 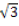cm, então o volume desse cubo é:

• A.

  24 cm³

• B.

  36 cm³.

• C.

  144 cm³.

• D.

  216 cm³.

O comprimento de uma circunferência qualquer, pode ser calculado pelo produto entre o diâmetro dessa circunferência e o valor de Pi (constante de Arquimedes representada pela letra do alfabeto grego π). Sabendo disso, um fazendeiro que deseja cercar uma área circular de raio igual a 20 m, deverá construir:

• A. 40π metros de cerca;
• B. 20π metros de cerca;
• C. 10π metros de cerca;
• D. 120π metros de cerca;
• E. 100π metros de cerca.

Um tanque na forma de um hexaedro regular com capacidade de armazenamento para 20 m³, está com 75% de sua capacidade preenchida com água. O volume de água que deve ser despejado dentro do tanque, a fim de enchê-lo completamente é:

• A.

  15 000 litros;

• B.

  5 000 litros;

• C.

  2 500 litros;

• D.

  500 litros;

• E.

  5 litros.