Questões sobre Números reais e complexos

Aordem decrescente correta de alguns números naturais está na alternativa:

• A. 36 ; 25 ; 14 ; 9 ; 18
• B. 40 ; 16 ; 9 ; 7 ; 1
• C. 48 ; 19 ; 23 ; 12 ; 6
• D. 106 ; 16 ; 6 ; 0 ; 1

A alternativa que contém somente números pares é:

• A.

  8, 16, 23, 34, 41, 50.

• B.

  8, 12, 18, 21, 23, 26.

• C.

  8, 10, 56, 90, 110, 330.

• D.

  8, 9, 10, 120, 180, 310.

Assinale a alternativa que contém apenas números ímpares:

• A.

  7, 11, 3, 5, 1, 13.

• B.

  20, 11, 5, 12, 28, 30.

• C.

  1, 3, 5, 7, 10, 13.

• D.

  20, 30, 40, 60, 80, 90.

Hoje, o Serviço de Meteorologia afirmou que, em Maria da Fé, a temperatura está a -6ºC. Carlos disse que irá aproveitar o tempo e dar um passeio com uma roupa mais leve. Ele está certo? Por quê?

• A.

  Carlos está certo, porque essa temperatura é temperada.

• B.

  Carlos está certo, porque essa temperatura é muito agradável.

• C.

  Carlos está errado, porque essa temperatura é muito fria.

• D.

  Carlos está errado, porque essa temperatura é muito quente.

Assinale a afirmação falsa.

• A.

  O produto de um número racional não nulo por um número irracional é sempre um número irracional.

• B.

  A soma de um número racional com um número irracional é sempre um número irracional.

• C.

  Entre dois números irracionais distintos sempre existe um número racional.

• D.

  Entre dois números racionais distintos sempre existe um número irracional.

• E.

  A soma de dois números irracionais é sempre um número irracional.

O inverso do número complexo 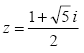 é:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Em relação aos seguintes números complexos a=1+i, b=1-i e c=-1-i, considere as seguintes afirmações:

I) As imagens de a, b e c no plano cartesiano são vértices de um triângulo.

II) a.b.c = -1+i

III) a + b + c = 1 - i IV) a e c são conjugados

São verdadeiras as afirmações:

• A.

  I e II

• B.

  II e IV

• C.

  I e III

• D.

  III e IV

• E.

  II e III

Observe a folha que a professora de Matemática distribuiu a cada um de seus alunos da 8ª A e o que ela disse em seguida.

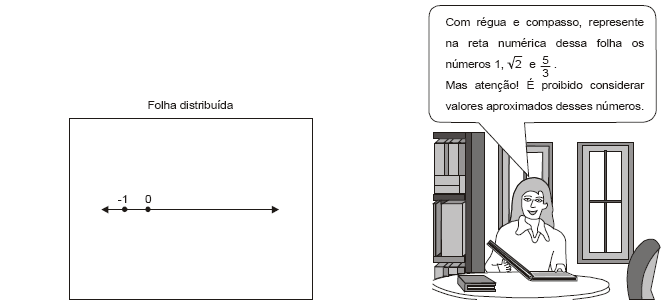
Com essa pequena atividade, a professora mostra que considera "Construções Geométricas" como uma ferramenta

• A.

  que permite integrar conhecimentos de geometria e de números.

• B.

  que deve ser trabalhada de modo independente de grandezas e medidas.

• C.

  adequada para desenvolver o ensino de probabilidades.

• D.

  indispensável no desenvolvimento do ensino e aprendizagem das unidades de medida de massa e volume e suas relações.

• E.

  que deve ser trabalhada pelo professor de Educação Artística, em Desenho Geométrico.

Um professor propôs a seus alunos de 5a série o seguinte problema:

Paulo e Luana, professores das 5as séries de uma escola resolveram elaborar as questões de uma prova para todas essas séries, de modo que Paulo se incumbiu das questões de número ímpar e Luana as de número par, em igual quantidade. Assim, pode-se concluir que o número que identificou a última questão dessa prova é, com certeza,

I. múltiplo de 3.
II. um número primo diferente de 2.
III. um número par.
IV. um número fracionário.

Com tal problema, é possível que esse professor tenha tido a intenção de levar seus alunos a

• A.

  identificar os múltiplos de 3, observando regularidades na seqüência de tais múltiplos.

• B.

  trabalhar com potências de números naturais com expoentes inteiros.

• C.

  reconhecer e relacionar propriedades dos números fracionários.

• D.

  estabelecer relações quantitativas entre subconjuntos do conjunto dos números naturais.

• E.

  decompor números naturais em seus fatores primos.

Considerando que, para todo número inteiro n, as potências da unidade imaginária i podem ser calculadas através das expressões i4n = 1; i4n+1 = i; i4n+2 = −1 e i4n+3 = −i, é correto afirmar que o valor da soma i−3 + i11 + i207 + i418 é

• A. 0
• B. i
• C. − i
• D. − 1 − i
• E. − 1 + i