Questões de Raciocínio lógico do ano 2013

Assinale qual é a contraditória do enunciado: Todo homem é mortal.

• A.

  Algum homem é mortal.

• B.

  Algum homem não é mortal.

• C.

  Algum mortal não é homem

• D.

  Nenhum homem é mortal.

• E.

  Nenhum mortal é homem.

Para as questões de números 62 a 64, considere a seguinte notação para os conectivos lógicos: ~ (para a negação), ∨ (para a disjunção inclusiva), & (para a conjunção) e ⊃ (para a implicação material).

Assinale qual das formas sentenciais seguintes é equivalente à forma:

~P ∨ Q

• A.

  P ⊃ Q

• B.

  (P ∨ ~Q) ⊃ Q

• C.

  (P & Q) ⊃ P

• D.

  ~~P ∨ ~Q

• E.

  P & ~Q

Para as questões de números 62 a 64, considere a seguinte notação para os conectivos lógicos: ~ (para a negação), ∨ (para a disjunção inclusiva), & (para a conjunção) e ⊃ (para a implicação material).

Assinale qual das seguintes formas sentenciais é uma tautologia.

• A.

  X ⊃ (X & Y)

• B.

  ~X & ~~X

• C.

  Y ⊃ (X ⊃ Y)

• D.

  X & (Y ∨ X)

• E.

  Y ⊃ (Y ⊃ X)

Para as questões de números 62 a 64, considere a seguinte notação para os conectivos lógicos: ~ (para a negação), ∨ (para a disjunção inclusiva), & (para a conjunção) e ⊃ (para a implicação material).

• A.

  O mesmo valor de A ∨ B.

• B. O valor de verdade não pode ser determinado.
• C.

  Verdadeiro.

• D.

  Falso.

• E.

  O mesmo valor de ~M & ~N.

Sobre as tabelas de verdade dos conectivos de disjunção (inclusiva), conjunção e implicação (material), assinale a alter nativa correta.

• A.

  As conjunções só são falsas quando ambos os conjuntos são falsos.

• B.

  Não existe implicação falsa com antecedente verdadeiro.

• C.

  As disjunções são falsas quando algum dos disjuntos é falso.

• D.

  Só há um caso em que as implicações são verdadeiras.

• E.

  As implicações são verdadeiras quando o antecedente é falso.

Considere que as seguintes proposições sejam verdadeiras.

I Se o dólar subir, as exportações aumentarão ou as importações diminuirão.

II Se as exportações aumentarem e as importações diminuírem, a inflação aumentará.

III Se o BACEN aumentar a taxa de juros, a inflação diminuirá.

Com base apenas nessas proposições, julgue os itens a seguir.

Suponha que o aumento da taxa de juros diminua o consumo, e o decréscimo do consumo diminua as importações. Nessa situação, é possível que juros e exportações aumentem na mesma época.

• C. Certo
• E. Errado

Considere que as seguintes proposições sejam verdadeiras.

I Se o dólar subir, as exportações aumentarão ou as importações diminuirão.

II Se as exportações aumentarem e as importações diminuírem, a inflação aumentará.

III Se o BACEN aumentar a taxa de juros, a inflação diminuirá.

Com base apenas nessas proposições, julgue os itens a seguir.

Se o dólar subir, então a inflação diminuirá.

• C. Certo
• E. Errado

Considere que as seguintes proposições sejam verdadeiras.

I Se o dólar subir, as exportações aumentarão ou as importações diminuirão.

II Se as exportações aumentarem e as importações diminuírem, a inflação aumentará.

III Se o BACEN aumentar a taxa de juros, a inflação diminuirá.

Com base apenas nessas proposições, julgue os itens a seguir.

Se o BACEN aumentar a taxa de juros, então as exportações não aumentarão ou as importações não diminuirão.

• C. Certo
• E. Errado

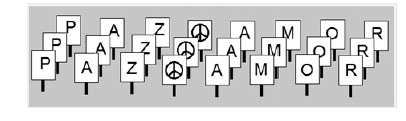
A partir da sequência de placas apresentada na figura acima, é correto concluir que a quantidade de maneiras distintas de trocar entre si as posições das placas e ainda obter a mesma formação inicial é igual a

• A.

  3⁸.

• B.

  6! × 6⁶.

• C.

  6⁸.

• D.

  (6!)² × 6⁴.

• E.

  (6!)⁶ × 6².

P1: Se a impunidade é alta, então a criminalidade é alta.

P2: A impunidade é alta ou a justiça é eficaz.

P3: Se a justiça é eficaz, então não há criminosos livres.

P4: Há criminosos livres.

C: Portanto a criminalidade é alta.

Considerando o argumento apresentado acima, em que P1, P2, P3 e P4 são as premissas e C, a conclusão, julgue os itens subsequentes.

A negação da proposição P1 pode ser escrita como “Se a impunidade não é alta, então a criminalidade não é alta.”

• C. Certo
• E. Errado