Questões sobre Disjunção: p ou q (representação p v q)

Considere que as letras P, Q, R e S representam proposições e que os símbolos 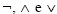 são operadores lógicos que constroem novas proposições e significam não, e e ou respectivamente. Na lógica proposicional, cada proposição assume um único valor (valor-verdade) que pode ser verdadeiro (V) ou falso (F), mas nunca ambos. Considerando que P, Q, R e S são proposições verdadeiras, julgue os itens seguintes.

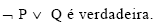
• C. Certo
• E. Errado

André é inocente ou Beto é inocente. Se Beto é inocente, então Caio é culpado. Caio é inocente se e somente se Dênis é culpado. Ora, Dênis é culpado. Logo

• A.

  Caio e Beto são inocentes

• B.

  André e Caio são inocentes

• C.

  André e Beto são inocentes

• D.

  Caio e Dênis são culpados

• E.

  André e Dênis são culpados

Ana é artista ou Carlos é carioca. Se Jorge é juiz, então Breno não é bonito. Se Carlos é carioca, então Breno é bonito. Ora, Jorge é juiz. Logo:

• A.

  a) Jorge é juiz e Breno é bonito

• B.

  Carlos é carioca ou Breno é bonito

• C.

  Breno é bonito e Ana é artista

• D.

  Ana não é artista e Carlos é carioca

• E.

  Ana é artista e Carlos não é carioca

O Teorema Fundamental da Aritmética afirma que:

Julgue se cada um dos itens subseqüentes reescreve, de modo correto e equivalente, o enunciado acima.

Ou n não é um número natural diferente de 1, ou n tem uma decomposição como um produto de fatores primos, que é única, a menos da ordem dos fatores.

• C. Certo
• E. Errado

M = 2x + 3y, então M = 4p + 3r. Se M = 4p + 3r, então M = 2w – 3r. Por outro lado, M = 2x + 3y, ou M = 0. Se M = 0, então M+ H = 1. Ora, M+H ≠ 1. Logo,

• A. 2w – 3r = 0
• B. 4p + 3r ≠ 2w – 3r
• C. M ≠ 2x + 3y
• D. 2x + 3y ≠ 2w – 3r
• E. M = 2w – 3r

Se X ≥ Y, então Z > P ou Q ≤ R. Se Z > P, então S ≤ T. Se S ≤ T, então Q ≤ R. Ora, Q > R, logo:

• A. S > T e Z ≤ P
• B. S ≥ T e Z > P
• C. X ≥ Y e Z ≤ P
• D. X > Y e Z ≤ P
• E.

  X < Y e S < T