Questões de Raciocínio lógico da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

 

A partir das informações dos textos I e II, julgue os itens subseqüentes.

Considere que as proposições "Todo advogado sabe lógica" e "Todo funcionário do fórum é advogado" são premissas de uma argumentação cuja conclusão é "Todo funcionário do fórum sabe lógica". Então essa argumentação é válida.

• C. Certo
• E. Errado

 A partir das informações contidas nos textos I e II, julgue os itens seguintes.

Se P e Q são proposições quaisquer, então uma proposição da forma tem somente valor lógico verdadeiro, isto é, essa proposição é uma tautologia.

• C. Certo
• E. Errado

Toda proposição da forma  é uma tautologia, isto é, tem somente a valoração V.

• C. Certo
• E. Errado

Os princípios de contagem, na matemática, incluem:

I Princípio da Soma: se um evento E₁ pode ocorrer de N₁ maneiras distintas, E₂, de N₂ maneiras distintas, ..., E_k, de N_k maneiras distintas, e se quaisquer dois eventos não podem ocorrer simultaneamente, então um dos eventos pode ocorrer em N₁ + N₂ + ... + N_k maneiras distintas.

II Princípio da Multiplicação: considere que E₁, E₂, ..., Ek são eventos que ocorrem sucessivamente; se o evento E₁ pode ocorrer de N₁ maneiras distintas, o evento E₂ pode ocorrer de N₂ maneira distintas, ..., o evento E_k pode ocorrer de N_k maneiras distintas, então todos esses eventos podem ocorrer, na ordem indicada, em N₁ × N₂ × ... × N_k maneiras distintas.

Considerando o texto acima e a informação do portal www.mp.to.gov.br, de que, no Ministério Público do Estado do Tocantins (MPE/TO), há 85 promotores de justiça e 12 procuradores de justiça, julgue os itens de 44 a 48.

Há 70 maneiras diferentes de se constituir um comitê que contenha exatamente 4 membros escolhidos de uma lista de 8 procuradores de justiça.

• C. Certo
• E. Errado

Os princípios de contagem, na matemática, incluem:

I Princípio da Soma: se um evento E₁ pode ocorrer de N₁ maneiras distintas, E₂, de N₂ maneiras distintas, ..., E_k, de N_k maneiras distintas, e se quaisquer dois eventos não podem ocorrer simultaneamente, então um dos eventos pode ocorrer em N₁ + N₂ + ... + N_k maneiras distintas.

II Princípio da Multiplicação: considere que E₁, E₂, ..., Ek são eventos que ocorrem sucessivamente; se o evento E₁ pode ocorrer de N₁ maneiras distintas, o evento E₂ pode ocorrer de N₂ maneira distintas, ..., o evento E_k pode ocorrer de N_k maneiras distintas, então todos esses eventos podem ocorrer, na ordem indicada, em N₁ × N₂ × ... × N_k maneiras distintas.

Considerando o texto acima e a informação do portal www.mp.to.gov.br, de que, no Ministério Público do Estado do Tocantins (MPE/TO), há 85 promotores de justiça e 12 procuradores de justiça, julgue os itens de 44 a 48.

Considere que, entre os promotores de justiça do MPE/TO, haja 27 mulheres. Suponha que 60 promotores tenham menos de 50 anos, e que, neste grupo, haja 15 mulheres. Nessa situação, um dos eventos "ter menos de 50 anos" ou "ser mulher" tem 72 maneiras distintas de ocorrer.

• C. Certo
• E. Errado

Os princípios de contagem, na matemática, incluem:

I Princípio da Soma: se um evento E₁ pode ocorrer de N₁ maneiras distintas, E₂, de N₂ maneiras distintas, ..., E_k, de N_k maneiras distintas, e se quaisquer dois eventos não podem ocorrer simultaneamente, então um dos eventos pode ocorrer em N₁ + N₂ + ... + N_k maneiras distintas.

II Princípio da Multiplicação: considere que E₁, E₂, ..., Ek são eventos que ocorrem sucessivamente; se o evento E₁ pode ocorrer de N₁ maneiras distintas, o evento E₂ pode ocorrer de N₂ maneira distintas, ..., o evento E_k pode ocorrer de N_k maneiras distintas, então todos esses eventos podem ocorrer, na ordem indicada, em N₁ × N₂ × ... × N_k maneiras distintas.

Considerando o texto acima e a informação do portal www.mp.to.gov.br, de que, no Ministério Público do Estado do Tocantins (MPE/TO), há 85 promotores de justiça e 12 procuradores de justiça, julgue os itens de 44 a 48.

Considere que se deseje eleger, entre os procuradores e os promotores do MPE/TO, um presidente, um vice-presidente e um ouvidor, para a direção de um clube dos membros do MPE/TO, de modo que nenhuma pessoa possa ser eleita para mais de um cargo. Nessa situação, é correto afirmar que há 288 maneiras diferentes de se escolherem os três membros para a direção do clube e este resultado é uma conseqüência do Princípio da Soma.

• C. Certo
• E. Errado

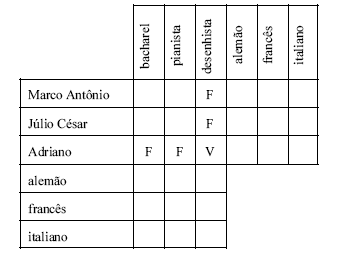
Na tabela acima, está marcada com V (verdadeiro) a célula que faz o cruzamento da seguinte informação: Adriano é desenhista. Considerando que a correspondências entre os nomes de pessoas, profissões e idiomas que falam sejam biunívocas, isto é, cada pessoa fala um e somente um idioma e exerce uma e somente uma profissão, e que Marco Antônio, Júlio César e Adriano têm profissões distintas e falam diferentes idiomas, julgue os itens subseqüentes, com base nessas informações e na marcação inicial especificada acima.

Se o pianista fala alemão e o bacharel fala francês, então Marco Antônio é bacharel e Júlio César é pianista é uma implicação verdadeira.

• C. Certo
• E. Errado

Considerando as informações apresentadas acima, julgue os itens subseqüentes.

Ao empregar os símbolos P, Q e R para as proposições primitivas "Paulo lê revistas científicas", "Paulo lê jornais" e "Paulo lê gibis" respectivamente, é correto simbolizar a proposição composta "Paulo lê gibis ou não lê jornais e não lê revistas científicas" por ¬((R  Q)  ¬P).

• C. Certo
• E. Errado

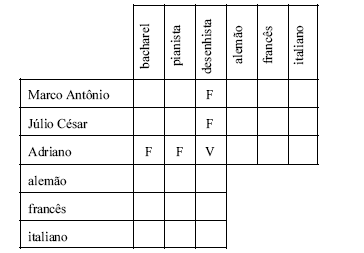
Na tabela acima, está marcada com V (verdadeiro) a célula que faz o cruzamento da seguinte informação: Adriano é desenhista. Considerando que a correspondências entre os nomes de pessoas, profissões e idiomas que falam sejam biunívocas, isto é, cada pessoa fala um e somente um idioma e exerce uma e somente uma profissão, e que Marco Antônio, Júlio César e Adriano têm profissões distintas e falam diferentes idiomas, julgue os itens subseqüentes, com base nessas informações e na marcação inicial especificada acima.

É verdadeira a proposição: Se o bacharel fala alemão e Marco Antônio fala italiano, então o pianista fala francês.

• C. Certo
• E. Errado

Com os algarismos 1, 2, 4, 5, 6 e 8 deseja-se formar números de 3 algarismos, não sendo permitida a repetição de algarismos em um mesmo número. Julgue os itens subseqüentes com relação a esses números.

Escolhendo-se um desses números ao acaso, a probabilidade de ele ser menor que 300 é superior a 0,3.

• C. Certo
• E. Errado