Questões sobre Econometria

Ruth foi ao médico e este receitou uns comprimidos que deviam ser cortados para tomar metade no café da manhã e metade no jantar. Ela foi para casa, jantou, cortou um comprimido e tomou a metade. Na manhã seguinte tomou a metade que sobrou e deu sequência ao tratamento, tendo o cuidado de só cortar um comprimido quando não havia nenhuma metade cortada anteriormente. Um dia, quase na hora do jantar, ela percebeu que havia esquecido de tomar o remédio algumas vezes. Ruth contou os comprimidos restantes tendo encontrado 7,5. Fez uns cálculos e descobriu o número de esquecimentos. Sabendo-se que este número está entre os cinco abaixo, pode-se afirmar que ele é:

• A.

  2;

• B.

  8;

• C.

  6;

• D.

  4;

• E.

  5.

Se o Var de 1 dia, com 95% de confiança, obtido por meio de um método não paramétrico, for equivalente a R$ 5.800,00, pode-se dizer que:

• A.

  em 5% das ocorrências, a perda será maior que R$ 5.800,00;

• B.

  a perda será no máximo no valor de R$ 5.800,00;

• C.

  a perda máxima será 5% maior do que R$ 5.800,00;

• D.

  em um mês não é possível perder mais do que R$ 5.800,00;

• E.

  na quinzena seguinte a perda máxima será de R$ 5.800,00.

A respeito das medidas de tendência central e de dispersão de uma distribuição de probabilidades, verifica-se que a(o)

• A.

  moda é sempre maior que a média.

• B.

  mediana é sempre menor que o desvio padrão.

• C.

  variância é sempre o dobro do desvio padrão.

• D.

  variância é uma medida de tendência central.

• E.

  desvio padrão é uma medida de dispersão.

• A.

  de mínima variância

• B.

  não tendencioso

• C.

  inconsistente

• D.

  linear

• E.

  suficiente

Se os dados de X e Z forem correlacionados negativamente, a estimação poderá ter problemas de

• A.

  autocorrelação dos resíduos

• B.

  heterocedasticidade

• C.

  homocedasticidade

• D.

  multicolinearidade

• E.

  linearidade

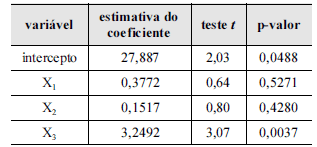
Uma empresa de transporte de cargas deseja expandir seus negócios e para isso fez um levantamento acerca das 48 empresas concorrentes. Foi considerado um modelo de regressão linear múltipla, em que a variável dependente Y representa o faturamento dessas empresas, havendo três variáveis explicativas — X₁, X₂ e X₃ — que representam um perfil dessas concorrentes. O ajuste foi efetuado por mínimos quadrados ordinários e os resultados são mostrados na tabela acima. Com base nessas informações, julgue os itens subsecutivos.

Os gráficos de dispersão permitem efetuar diagnósticos acerca da hipótese de linearidade do modelo ajustado.

• C. Certo
• E. Errado

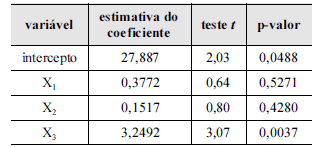
Uma empresa de transporte de cargas deseja expandir seus negócios e para isso fez um levantamento acerca das 48 empresas concorrentes. Foi considerado um modelo de regressão linear múltipla, em que a variável dependente Y representa o faturamento dessas empresas, havendo três variáveis explicativas — X₁, X₂ e X₃ — que representam um perfil dessas concorrentes. O ajuste foi efetuado por mínimos quadrados ordinários e os resultados são mostrados na tabela acima. Com base nessas informações, julgue os itens subsecutivos.

O modelo de regressão linear múltipla em questão pode ser representado na forma matricial y = XB + g, em que y é um vetor 48 × 1, X é a matriz de delineamento cuja dimensão é 48 × 3, B é o vetor de coeficientes 3 × 1 e g é um vetor aleatório 48 × 1.

• C. Certo
• E. Errado

Uma regressão linear simples, Y = a + bX, é estimada pelo método de minimização da soma dos quadrados dos erros, relacionando dois conjuntos de dados X e Y. Os parâmetros estimados são a e b. Nesse contexto, NÃO é correto afirmar que a(o)

• A.

  soma dos resíduos será nula.

• B.

  reta estimada passará pelo ponto  onde e são as médias dos dados X e dos dados Y.

• C.

  estimativa de b será negativa, se o coeficiente de correlação entre os dados X e Y for negativo.

• D.

  distribuição de probabilidade do estimador de b é normal.

• E.

  método usado não minimiza a soma dos valores absolutos dos resíduos.

O preço de uma ampla cesta de bens e serviços, em certa data, era de R$ 1.600,00, sendo a ele atribuído um número índice de 100. O preço da mesma cesta, um mês após, com os mesmos bens e serviços em iguais quantidades, era de R$ 1.616,00, sendo a ele atribuído um índice de 101. A partir desses dados, conclui-se que

• A.

  a inflação no período, de acordo com o índice calculado, foi de 101%.

• B.

  a estimativa do índice de preço se baseou na metodologia de Laspeyres.

• C.

  a metodologia usada no cálculo do índice foi a de Paasche.

• D.

  foi calculado um índice de quantidade que mostra uma inflação de 1% no mês.

• E.

  seria necessário mudar as quantidades de bens e serviços na cesta para refletir a inflação verdadeira.

Os parâmetros a e b da regressão linear simples, Y = a + bX, entre dois conjuntos de dados Y e X, foram estimados pelo método de minimização da soma dos quadrados dos desvios. No gráfico cartesiano comum, com os dados X no eixo horizontal e os dados Y no eixo vertical, a reta de regressão estimada

• A.

  passará pelo ponto (X _min , Y _min), onde X _min e Y _min são os valores mínimos dos conjuntos de dados X e Y, respectivamente.

• B.

  passará pelo ponto (X_i, Yi), para algum i, onde i indica as iésimas observações dos conjuntos de dados X e Y, respectivamente.

• C.

  interceptará o eixo vertical na origem (0,0), se a estimativa do parâmetro b for positiva.

• D.

  será vertical, se o coeficiente de correlação entre os dados dos conjuntos X e Y for igual a 1.

• E.

  será horizontal, se o coeficiente de correlação entre os dados dos conjuntos X e Y for nulo.