Questões de Engenharia Mecânica do ano 2004

Considere a mudança de estado de líquido saturado para vapor saturado de uma substância pura que obedece à seguinte relação termodinâmica

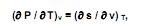
em que P, T, v e s denotam pressão, temperatura, volume específico e entropia específica, respectivamente.

Para estados termodinâmicos na região de saturação, a diferença de entalpia do vapor (h_v) e do líquido (h_l), representada por h_lv = h_v - h_l, pode ser determinada a partir da inclinação ß = (d P / dT)_sat da curva de pressão de vapor e da diferença dos volumes específicos vapor saturado - líquido v_lv = v_v - v_l à temperatura dada. Marque a opção que fornece a expressão correta para o cálculo da diferença de entalpia vapor líquido saturado.

• A.

  h_lv = ß T v_lv

• B.

  h_lv = ß ^1/2 T v_lv

• C.

  h_lv = (ß T) ^1/2 v_lv

• D.

  h_lv = (2 ß) ^1/2 T v_lv

• E.

  h_lv = 2 ß T v_lv

Assinale a opção incorreta.

• A.

  Em sistemas termodinâmicos que realizam um determinado processo, tanto o trabalho como o calor envolvidos na mudança de um estado inicial 1 para um estado final 2 dependem dos estados intermediários pelos quais o sistema passou. A diferença entre eles, porém, independe dos estados intermediários e depende apenas dos estados termodinâmicos dos pontos 1 e 2.

• B.

  Uma pequena usina termoelétrica opera em um local onde a temperatura ambiente é de 27°C. Sua fonte quente encontra-se a 627°C e fornece 1MW para um motor, que consegue produzir 450kW de trabalho. Se essa máquina operasse em um ciclo de Carnot, a rejeição de calor para o meio ambiente local seria aproximadamente 217kW menor que a rejeição atual.

• C.

  Para um gás ideal, a diferença dos calores específicos a pressão e a volume constante, C_p e C_v respectivamente, é a constante do gás.

• D.

  A disponibilidade de um sistema termodinâmico é definida como sendo a quantidade de trabalho obtido se o sistema realizasse um processo termodinâmico cujo estado final esteja em equilíbrio térmico com sua vizinhança. A diferença  entre dois estados termodinâmicos 1 e 2 está associada ao trabalho total envolvido em um processo irreversível que liga o estado 1 ao estado 2.

• E.

  Um quilo de hélio, à temperatura ambiente, encontra- se em um cilindro com um êmbolo. O cilindro é termicamente isolado e o êmbolo pode mover-se livremente. Calor é adicionado ao sistema a uma taxa constante. Depois de um certo tempo, cessa-se o suprimento de calor, o êmbolo é travado em sua posição final, e o isolamento térmico é retirado, de forma que o sistema pode trocar calor livremente com o meio ambiente. A temperatura do meio ambiente manteve-se constante durante todo o processo. Esperado o tempo adequado para que haja equilíbrio térmico entre o sistema e o meio ambiente, a curva no diagrama Pressão-Volume para esse processo é a apresentada abaixo.

  

Um eixo de raio "a" gira a 240 rpm num mancal com folga radial 10^-3 a. A tensão de cisalhamento em (N/m² ) em uma lâmina de óleo de viscosidade µ é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

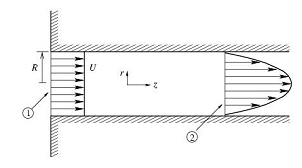
A figura a seguir ilustra um escoamento incompressível e laminar em um duto circular de raio R. O escoamento desenvolve-se a partir de um perfil uniforme com velocidade U até adquirir, na seção 2, um perfil de velocidades na forma de um parabolóide

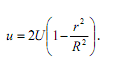
Sendo 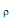 a massa específica do fluido e denotando por p₁ e p₂ as pressões nas seções 1 e 2, respectivamente, a força de arrasto F que as paredes do duto exercem sobre o fluido é igual a

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Um analista pericial construiu um modelo de projétil na escala 1:8 que apresenta um coeficiente de arrasto 3 para um número de Mach igual a 2, correspondendo a um movimento em ar à temperatura ambiente. Considere o ar comportando-se como gás ideal. Um protótipo desse modelo foi disparado com o mesmo número de Mach em ar,à mesma temperatura e cuja a massa específica foi igual à metade daquela do ar no escoamento do modelo. Nessas condições a força de resistência do ar sobre o protótipo é

• A.

  32 vezes maior.

• B.

  8 vezes maior.

• C.

  16 vezes maior.

• D.

  128 vezes maior.

• E.

  64 vezes maior.

O transportador de correia ilustrado na figura abaixo está montado em um navio e é usado para recolher contaminantes superficiais indesejáveis como óleo flutuando na água do mar.

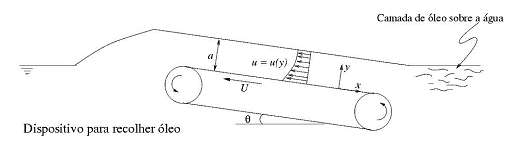
 Admita que a lâmina de óleo seja suficientemente espessa para considerar que o dispositivo opere com fornecimento ilimitado desse líquido. Suponha também que a correia opera com velocidade U constante e o escoamento em questão é unidirecional e permanente. Com relação à vazão de óleo por unidade de largura da correia transportadora que pode ser recolhida é correto afirmar que

• A.

  a vazão q é diretamente proporcional ao ângulo de inclinação  da correia.

• B.

  a vazão q aumenta com o quadrado da distância transversal "a".

• C.

  a vazão q independe da massa específica do líquido.

• D.

  a diferença (q - Ua ) é diretamente proporcional ao produto a sen .

• E.

  a vazão é sempre igual a Ua para   em que n=0, 1, 2, ...

Escoamentos a elevados números de Reynolds são caracterizados por terem uma fraca influência dos efeitos viscosos em sua dinâmica. Mesmo nesses tipos de escoamentos, porém, quando um fluido real escoa próximo a uma parede, os efeitos viscosos tornam-se importantes em uma pequena região chamada de cama da limite. Formalmente, a camada limite é definida como sendo a região, de espessura local 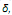  compreendida entre uma parede, na qual o fluido está aderido, e a camada de fluido na qual a velocidade local do escoamento é de 99% da velocidade do escoamento livre Nessa região, para o caso de escoamento bidimensional sem gradiente de pressão, as equações de Navier Stokes podem ser simplificadas se são usadas as seguintes variáveis de similaridade,

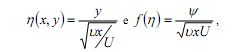
em que 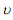 é a viscosidade cinemática do fluido, U é velocidade da corrente livre fora da camada limite,  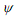 é a função de corrente do escoamento, tal que  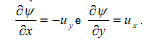Aqui, o vetor velocidade do escoamento é definido como sendo u=(u_x, u_y). Considere um escoamento uniforme com velocidade U sobre uma placa plana de comprimento L e largura 1 m. A tensão de cisalhamento agindo sobre a placa é aproximadamente  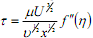 em que µ é a viscosidade dinâmica do fluido e  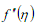 a segunda derivada da função f (n) com relação a (n). O número de Reynolds deste escoamento é definido por  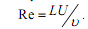A força de arrasto viscoso agindo sobre toda a placa, dividida por µU é dada por:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Um material combustível é compactado a L=3 metros de espessura e em seguida armazenado em um depósito apropriado de segurança máxima (ver figura abaixo para detalhes).

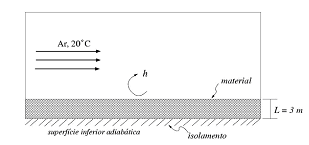
A taxa de geração interna de calor na pilha de material provocada por reações químicas entre as partículas que compõem o material e os gases atmosféricos é igual a 20 Watts/m³ . A temperatura no ambiente de armazenamento é 20 °C e o coeficiente de transferência de calor por convecção h na superfície externa (interface material-ambiente) é igual a 4 W/m² K. Admitindo que o processo de transferência de calor é unidimensional e que o regime é permanente, a temperatura na superfície superior da pilha do material, em graus Celsius, tem o valor de

• A.

  25ºC.

• B.

  35ºC.

• C.

  45ºC.

• D.

  55ºC.

• E.

  65ºC.

Um modelo de transferência de calor para uma primeira estimativa da espessura da placa de resíduos depositada nos dentes de um indivíduo admite que ao longo do tempo a superfície do dente fica coberta por uma camada fina sólida formada pelos resíduos depositados devido a fluxos de alimentos e ingestão de líquidos.

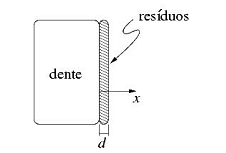
Considere que a condutividade térmica média dos resíduos presente na placa seja igual a (1/5) W/m K, que o fluxo específico de calor na superfície seja 1000 W/m² e que a diferença de temperatura entre as superfícies da camada de resíduos seja aproximadamente 5 °C. Assumindo o processo de transferência de calor unidimensional e em regime permanente, a espessura da placa em (mm) é

• A.

  0,5mm.

• B.

  1mm.

• C.

  2mm.

• D.

  3mm.

• E.

  4mm.

Suponha que o isolamento térmico de um tubo que transporta um fluido a temperaturas maiores do que a temperatura do meio ambiente deva ser escolhido. Para fundamentar sua escolha, o responsável pelo projeto modelou esse problema como sendo um problema de transferência de calor, em regime permanente, de um tubo cilíndrico de comprimento L , com raio interno r_i e raio externo r_e , no qual escoa um fluido à temperatura constante T_i . A temperatura do ambiente externo é T_e .  A parede do cilindro possui condutividade térmica k constante e não há, no sistema, nenhuma geração interna de calor. Dessa forma, a equação que descreve a distribuição de temperatura na parede do tubo reduz-se a

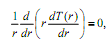
que após integração resulta em T(r) = C₁ln(r)+C ₂, em que as constantes C₁ e C₂ são determinadas com as condições de contorno adequadas ao problema. Com respeito à resistência térmica da parede do tubo, julgue os itens abaixo, marque com F a(s) afirmativa(s) falsa(s) e com V a(s) verdadeira(s) e assinale a opção correta.

( ) Para tubos de mesmo material e raios, aumentando- se o comprimento do tudo em 4 vezes, a resistência condutiva do tubo é reduzida em 4 vezes.

( ) A resistência térmica do tubo é diretamente proporcional à razão de aspecto r_e /r_i.

( ) Sejam dois tubos cilíndricos de mesmo comprimento e feitos do mesmo material, com razões de aspecto r_e /r_i iguais a a e a² . Portanto, a resistência térmica de um dos tubos é duas vezes maior do que a do outro.

• A.

  V,F,V

• B.

  F,V,F

• C.

  V,F,F

• D.

  V,V,F

• E.

  F,V,V