Questões de Engenharia Química

O Ferro metálico (Fe⁰) pode ser obtido a partir da redução de um óxido de ferro, como a hematita (Fe₂O₃), utilizando um agente redutor como o monóxido de carbono. Se 80 toneladas de uma amostra de minério de ferro com 80% de pureza (em termos de massa de hematita por massa total) forem processadas para a obtenção de ferro metálico, quantas toneladas de CO₂ serão lançadas na atmosfera?

M_Fe = 56 g/gmol

• A.

  52,8 ton.

• B.

  66,0 ton.

• C.

  35,2 ton.

• D.

  44,0 ton.

• E.

  48,0 ton.

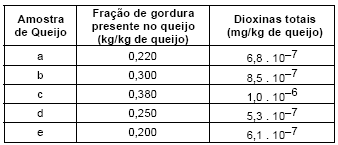
Um grupo de contaminantes muito perigoso para a saúde do ser humano é o das dioxinas. Considerando que a quantidade máxima tolerável de dioxinas presente nas gorduras encontradas em queijos são 3 ppt e que, em média, um quilo de queijo possui entre 180 g e 400 g de gorduras, determine quais das amostras de queijo, apresentadas abaixo, são impróprias para consumo humano.

• A.

  São impróprias as amostras b e e.

• B.

  São impróprias as amostras a, b e c.

• C.

  Apenas a amostra c é imprópria.

• D.

  Todas as amostras são impróprias.

• E.

  São impróprias as amostras a e e.

Em um processo industrial de descafeinação de café utilizando dióxido de carbono supercrítico, a área superficial das partículas de café moído é muito importante. Quanto maior esta área, menor a resistência à transferência de massa. Considerando que neste processo industrial normalmente utilizam-se partículas esféricas de café moído com 4 mm de diâmetro, o acréscimo na área superficial (em m²/kg de partículas) ao se utilizar partículas com diâmetros 50% menores será de:

Dados:

ρ_partículas = 1200 kg/m³

• A.

  0,67 m²/kg.

• B.

  1,00 m²/kg.

• C.

  1,25 m²/kg.

• D.

  2,00 m²/kg.

• E.

  2,50 m²/kg.

Considere as afirmativas abaixo sobre sabões e detergentes, compostos orgânicos utilizados em larga escala para remoção de gorduras.

I. Tanto as moléculas de sabão como as de detergente reagem com as gorduras quebrando a cadeia carbônica destes compostos e, desta forma, aumentando sua solubilidade em água.

II. A diferença entre detergentes sulfonados biodegradáveis e não-biodegradáveis são as estruturas das cadeias laterais, enquanto que no detergente biodegradável esta cadeia é linear, no detergente não biodegradável esta cadeia é ramificada.

III. Tanto as moléculas dos detergentes como as dos de sabões possuem uma parte hidrofílica e uma parte hidrofóbica.

IV. Na reação para a obtenção de sabão comum, os glicerídeos (gorduras de fonte animal) reagem com soda cáustica produzindo glicerol mais o sabão propriamente dito.

V. As moléculas de sabões e detergentes formam micelas com superfícies hidrofóbicas.

É correto o que se afirma APENAS em

• A.

  II, III, e IV.

• B.

  I, II e V.

• C.

  III e V.

• D.

  II, IV e V.

• E.

  I, II e III e IV.

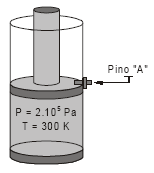
A figura abaixo descreve um sistema do tipo cilindropistão. Considere que não existe atrito entre o pistão e a parede do cilindro. Inicialmente a pressão no interior do cilindro é de 2 . 10⁵ Pa e a temperatura é 300 K. Calcule o trabalho necessário, por mol de gás no interior do cilindro, para que o sistema atinja a nova condição de equilíbrio após a retirada do pino "A". Considere também que o processo é isotérmico e que a pressão externa é a atmosférica (1 . 10⁵ Pa).

• A.

  −2494,2 J/mol

• B.

  −1728,8 J/mol

• C.

  −1247,1 J/mol

• D.

  1728,8 J/mol

• E.

  2494,2 J/mol

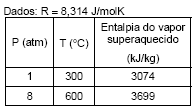
Uma turbina é alimentada com vapor superaquecido a 600 °C e 8 atm. A corrente de alimentação tem uma velocidade de 80 m/s e vazão mássica de 4,0 kg/s. A corrente de saída tem velocidade de 20 m/s, temperatura de 300 °C e pressão 1 atm. Se o equipamento opera em regime de estado estacionário, qual a máxima quantidade de trabalho possível de se extrair desta turbina?

• A.

  2500,0 kJ/s.

• B.

  2512,0 kJ/s.

• C.

  2506,0 kJ/s.

• D.

  2514,4 kJ/s.

• E.

  2524,0 kJ/s.

Determine a pressão de bolha (P^bolha) de uma mistura líquida contendo 20% de pentano, 50% hexano e 30% de heptano (em composição molar) e a fração molar de pentano (y_p) na fase vapor em equilíbrio com esta mistura líquida mantida a 60 °C. Nesta temperatura, as pressões de vapor do pentano, hexano e heptano são, respectivamente, 2,9; 1,1 e 0,4 bar.

• A.

  P^bolha = 1,25; y_p = 0,464.

• B.

  P^bolha = 1,79; y_p = 0,810.

• C.

  P^bolha = 1,79; y_p = 0,780.

• D.

  P^bolha = 1,25; y_p = 0,522.

• E.

  P^bolha = 1,79; y_p = 0,580.

Considere as afirmativas e a figura abaixo, que representa o diagrama de fases para uma substância pura.

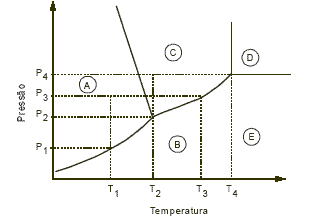
I. As regiões A, D e E representam regiões em que a substância seria um sólido, um fluido-supercrítico e um gás, respectivamente.

II. A temperatura e a pressão do ponto triplo desta substância são T₄ e P₄.

III. Se esta substância estiver inicialmente na temperatura e na pressão T₁ e P₃, ao elevar-se a temperatura até T₂, mantendo a pressão constante, mudase o estado de agregação da substância de sólido para líquido.

IV. A pressão P₁ é a pressão de liquefação na temperatura T₁, para esta substância.

V. A temperatura T₃ é a temperatura de ebulição desta substância na pressão P₃.

É correto o que se afirma APENAS em

• A.

  III, IV e V.

• B.

  II, III e V.

• C.

  I, II e IV.

• D.

  I, III e V.

• E.

  II e V.

Um grupo de pesquisadores mediu a variação da pressão de vapor do Argônio com a temperatura na vizinhança de 84 K e determinou a seguinte correlação: T B lnP^vap = A − B/T ; sendo A = 22,5 e B = 995,2 K. Determine a variação de entropia na mudança de fase (líquido-vapor) do argônio a 84 K.

Dados:

(R = 8,314 J/molK)

• A.

  2,2 J/molK.

• B.

  31,0 J/molK.

• C.

  98,5 J/molK.

• D.

  15,7.10² J.K/mol.

• E.

  69,5.10⁴ J.K/mol.

A Equação de Estado de van der Waals, 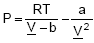 foi a primeira a predizer com relativo sucesso o equilíbrio transição líquido–vapor de substâncias puras. Sabendo que os coeficientes "a" e "b" são específicos para cada substância e não são dependentes nem da temperatura nem da pressão.

I. O coeficiente "b" da equação para uma dada substância, representa o menor volume possível que um mol desta substância pode assumir.

II. Em baixas temperaturas e altas pressões o resultado obtido através da equação de van der Waals para o volume molar tende a ser muito próximo do resultado obtido (para o volume molar) utilizando-se a equação dos gases ideais.

III. O termo (− a/V²) é o termo que leva em consideração as forças de atração entre as moléculas das substâncias puras.

IV. Esta é uma equação cúbica em V, em temperaturas abaixo da crítica, para uma mesma pressão de vapor a dada temperatura tem-se três raízes, a menor é o volume molar do líquido, a maior é o volume molar do vapor e a intermediária não tem sentido físico.

V. Para volumes molares muito grandes os resultado apresentados por esta equação tendem aos resultado obtidos pela equação dos gases ideais, em uma mesma temperatura.

É correto o que se afirma APENAS em

• A.

  II e V.

• B.

  I, IV, e V.

• C.

  II, III, e V.

• D.

  I, II, III, e IV.

• E.

  I, III, IV e V.