Questões de Engenharia (Teoria Geral) do ano 2011
Lista completa de Questões de Engenharia (Teoria Geral) do ano 2011 para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
A viscosidade absoluta, também conhecida como viscosidade dinâmica, é uma propriedade física característica de um dado fluido. Analisando-se a influência da temperatura sobre a viscosidade absoluta de líquidos e gases, observa-se que a(s)
- A.
variação da viscosidade com a temperatura é função da substância em si e não de seu estado físico.
- B.
viscosidade de líquidos aumenta e a de gases decresce com o aumento da temperatura.
- C.
viscosidade de líquidos decresce e a de gases aumenta com o aumento da temperatura.
- D.
viscosidades de líquidos e gases aumentam com o aumento da temperatura.
- E.
viscosidades de líquidos e gases decrescem com o aumento da temperatura.
Viscosidade de fluidos é comumente expressa em centipoise, apesar de sua unidade no sistema internacional de unidades ser Pa.s. Sabendo-se que centipoise (cP) é a centésima parte do Poise (P) e que Poise é g.cm−1.s−1, pode-se afirmar que um óleo com viscosidade igual a 30 cP tem uma viscosidade, expressa em Pa.s, igual a
- A.
0,003
- B.
0,03
- C.
0,3
- D.
3
- E.
30
Considere que a pressão absoluta em dado ambiente é expressa em termos de pressão manométrica, caso a pressão do ambiente seja maior que a pressão atmosférica local, ou em termos de vácuo, caso a pressão do ambiente seja menor que a pressão atmosférica local. Nesse sentido, a pressão
- A.
absoluta e o vácuo são iguais.
- B.
absoluta é igual à soma da pressão atmosférica local com o dobro do vácuo.
- C.
absoluta é igual à soma da pressão manométrica com o vácuo.
- D.
manométrica é a soma da pressão absoluta com a pressão atmosférica local.
- E.
atmosférica local é igual à diferença entre a pressão absoluta e a pressão manométrica.
Considere um fluido escoando em regime permanente, em uma tubulação, do ponto 1 ao ponto 2. Integrando-se a equação da conservação da quantidade de movimento (equação do movimento) entre esses dois pontos, ao longo de uma linha de corrente do fluido, para um fluido ideal (viscosidade nula e incompressível), obtém-se a Equação de Bernoulli. Essa equação afirma que a carga total, dada pela soma das cargas de pressão, de velocidade e de altura, é constante ao longo do escoamento. Observa-se, entretanto, que, para fluidos reais incompressíveis, essa carga total diminui à medida que o fluido avança através de uma tubulação, na ausência de uma bomba entre os pontos 1 e 2. Isso ocorre porque
- A.
a velocidade do fluido diminui à medida que o fluido avança do ponto 1 para o ponto 2.
- B.
parte da energia mecânica do fluido é transformada irreversivelmente em calor.
- C.
o fluido se resfria ao ser deslocado do ponto 1 para o ponto 2.
- D.
o ponto 2 está situado abaixo do ponto 1.
- E.
o ponto 2 está situado acima do ponto 1.
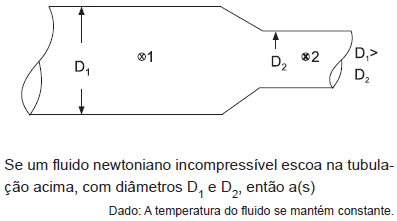
- A.
pressão no ponto 2 é maior que no ponto 1.
- B.
velocidade do fluido no ponto 2 é maior que no ponto 1.
- C.
viscosidade do fluido no ponto 2 é maior que no ponto 1.
- D.
densidade do fluido no ponto 2 é maior que no ponto 1.
- E.
velocidades do fluido nos pontos 1 e 2 são iguais.
- A.
T = 10 N
- B.
T = 13 N
- C.
T = 15 N
- D.
T = 18 N
- E.
T = 60 N
Uma barra homogênea de comprimento L = 1,0 m e seção reta quadrada, de lado 2,0 cm, está submetida a uma tração de 200 kN. O material do qual é constituída a barra possui módulo de elasticidade de 200 GPa. Qual o valor da deformação da barra, considerando que se encontra no regime elástico?
Dado: 1 GPa = 109 Pa
- A.
25 cm
- B.
2,5 cm
- C.
25 mm
- D.
2,5 mm
- E.
0,25 mm
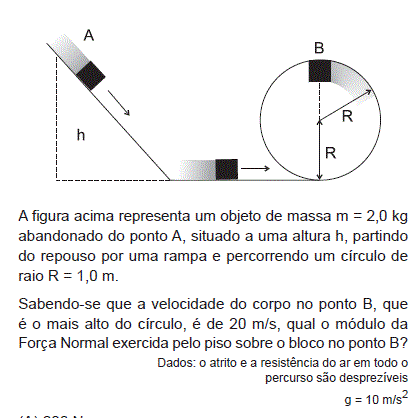
- A.
200 N
- B.
380 N
- C.
400 N
- D.
780 N
- E.
800 N
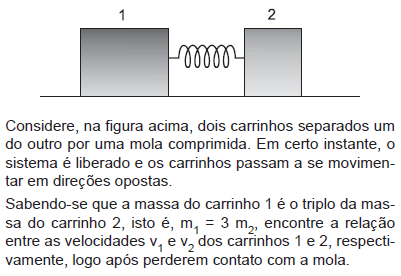
- A.
- B.
- C.
v1 = v2
- D.
v1 = 3v2
- E.
v1 = 4v2
Uma partícula de massa m está submetida a uma força variável no tempo, a qual produz uma aceleração nesse corpo dada por
a(t) = 2t
Encontre a equação de movimento para essa partícula, considerando que a velocidade inicial e a posição inicial são nulas, isto é, v0 = S0= 0.
- A.
- B.
S(t) = t3
- C.
- D.
- E.
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
