Questões de Estatística

Em decorrência do desenvolvimento urbano e tecnológico, tem-se a preocupação de monitorar os efeitos nocivos da poluição ambiental sobre a saúde da população urbana. A figura acima mostra o diagrama de caixa (box-plot) que descreve a distribuição da concentração de chumbo no sangue, em μg·dL!1, obtida com base em uma amostra aleatória de 200 pessoas do sexo masculino e de 100 pessoas do sexo feminino que trabalham em postos de combustível localizados em determinado município brasileiro. Com base nessas informações, julgue os itens de 106 a 111.

A distribuição das concentrações de chumbo encontradas no sangue das pessoas do sexo feminino que trabalham nesses postos de combustível apresenta intervalo interquartílico inferior àquele apresentado pela distribuição referente às pessoas do sexo masculino que trabalham nesses postos de combustível.

• C. Certo
• E. Errado

• A.
• B.

  

• C.

  40 e 10

• D.

  10 e 40

• E.

  

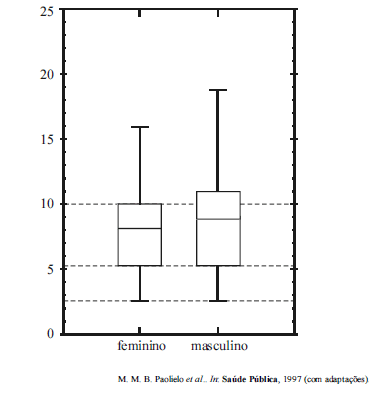
Em decorrência do desenvolvimento urbano e tecnológico, tem-se a preocupação de monitorar os efeitos nocivos da poluição ambiental sobre a saúde da população urbana. A figura acima mostra o diagrama de caixa (box-plot) que descreve a distribuição da concentração de chumbo no sangue, em μg·dL!1, obtida com base em uma amostra aleatória de 200 pessoas do sexo masculino e de 100 pessoas do sexo feminino que trabalham em postos de combustível localizados em determinado município brasileiro. Com base nessas informações, julgue os itens de 106 a 111.

• C. Certo
• E. Errado

O instrumento empregado para a medida da correlação linear de Pearson é o coeficiente de correlação. Esse coeficiente deve indicar o grau de intensidade da correlação entre duas variáveis e, ainda, o sentido dessa correlação. Assinale a alternativa que indica adequadamente a interpretação de um determinado resultado obtido r = 0,98 para o coeficiente de correlação de Pearson:

• A.

  Correlação linear positiva altamente significativa entre as variáveis.

• B.

  Correlação linear negativa altamente significativa entre as variáveis.

• C.

  Correlação linear positiva relativamente fraca entre as variáveis.

• D.

  Correlação linear positiva muito fraca entre as variáveis.

• E.

  Não há correlação linear positiva entre as variáveis.

Considere os eventos A, B, C e D, definidos abaixo, relativos ao número de veículos por família em determinada cidade.

A = uma família possui 1 ou mais veículos;

B = uma família possui 2 ou mais veículos;

C = uma família possui 3 ou mais veículos;

D = uma família possui 4 ou mais veículos.

Considere, ainda, que as probabilidades de ocorrência desses eventos são: P(A) = 0,9; P(B) = 0,6; P(C) = 0,3 e P(D) = 0. Com base nessas informações, julgue os itens que se seguem.

A probabilidade de uma família na referida cidade possuir exatamente 1 veículo é igual a 0,3.

• C. Certo
• E. Errado

• A.

  Devemos considerar uma amostra com 3 fumantes e 4 não fumantes.

• B.

  Devemos considerar uma amostra com 4 fumantes e 4 não fumantes.

• C.

  Devemos considerar uma amostra com 8 fumantes e 0 não fumantes.

• D.

  Devemos considerar uma amostra com 0 fumantes e 8 não fumantes.

• E.

  Devemos considerar uma amostra com 3 fumantes e 5 não fumantes.

Considere os eventos A, B, C e D, definidos abaixo, relativos ao número de veículos por família em determinada cidade.

A = uma família possui 1 ou mais veículos;

B = uma família possui 2 ou mais veículos;

C = uma família possui 3 ou mais veículos;

D = uma família possui 4 ou mais veículos.

Considere, ainda, que as probabilidades de ocorrência desses eventos são: P(A) = 0,9; P(B) = 0,6; P(C) = 0,3 e P(D) = 0. Com base nessas informações, julgue os itens que se seguem.

A probabilidade de uma família na referida cidade não possuir veículo é igual ou superior a 0,15.

• C. Certo
• E. Errado

• A.

  75kg e 65kg

• B.

  69kg e 55kg

• C.

  80kg e 55kg

• D.

  69kg e 60kg

• E.

  75kg e 60kg

Considere os eventos A, B, C e D, definidos abaixo, relativos ao número de veículos por família em determinada cidade.

A = uma família possui 1 ou mais veículos;

B = uma família possui 2 ou mais veículos;

C = uma família possui 3 ou mais veículos;

D = uma família possui 4 ou mais veículos.

Considere, ainda, que as probabilidades de ocorrência desses eventos são: P(A) = 0,9; P(B) = 0,6; P(C) = 0,3 e P(D) = 0. Com base nessas informações, julgue os itens que se seguem.

O número médio de veículos por família na referida cidade é igual ou superior a 2.

• C. Certo
• E. Errado

Considere os eventos A, B, C e D, definidos abaixo, relativos ao número de veículos por família em determinada cidade.

A = uma família possui 1 ou mais veículos;

B = uma família possui 2 ou mais veículos;

C = uma família possui 3 ou mais veículos;

D = uma família possui 4 ou mais veículos.

Considere, ainda, que as probabilidades de ocorrência desses eventos são: P(A) = 0,9; P(B) = 0,6; P(C) = 0,3 e P(D) = 0. Com base nessas informações, julgue os itens que se seguem.

A probabilidade condicional P(B*A) é inferior a 0,6.

• C. Certo
• E. Errado