Questões de Estatística

O elemento X₁ tem distribuição normal padrão.

• C. Certo
• E. Errado

Considere que Z seja uma variável aleatória normal padrão e que Y seja uma variável aleatória de Bernoulli com parâmetro p = 0,9. Considere também que a esperança condicional de Z para Y = 1 seja igual  a 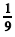 . Nessa situação, julgue os itens a seguir.

A covariância entre Z e Y é superior a 0,15.

• C. Certo
• E. Errado

Texto para as questões 21 e 22

No ano passado, a probabilidade de um indivíduo se tornar milionário no Brasil foi

• A.

  inferior a 0,0005.

• B.

  superior a 0,0005 e inferior a 0,0015.

• C.

  superior a 0,0015 e inferior a 0,0025.

• D.

  superior a 0,0025.

       Um estudo sobre a segmentação do mercado de trabalho comparou o salário daquele que trabalha por conta própria (Y, em R$ mil) com o salário daquele que tem a carteira assinada (X, em R$ mil). Foi ajustado um modelo de regressão linear na forma Y = ax + b + g, em que a e b são os coeficientes do modelo e g representa um erro aleatório com média zero e desvio-padrão  As estimativas de mínimos quadrados ordinários para os coeficientes a e b foram respectivamente iguais a 0,5 e R$ 6 mil. A quantidade de observações utilizadas para o ajuste do modelo foi igual a 400, e os desvios-padrão amostrais de Y e X foram, respectivamente, iguais a R$ 2 mil e R$ 1,5 mil.

Com base nessas informações, julgue os itens subseqüentes.

O coeficiente de determinação ajustado (ou R² ajustado) é superior a 0,15 (ou 15%).

• C. Certo
• E. Errado

O valor esperado de X X^N é uma matriz simétrica positiva semi-definida.

• C. Certo
• E. Errado

Considerando um vetor aleatório (X, Y) distribuído na função de densidade conjunta 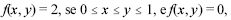caso contrário, julgue os itens a seguir.

A média de Y é inferior a 0,5.

• C. Certo
• E. Errado

Texto para as questões de 30 a 32

Considere que X ₁ , X ₂ , ..., X _n sejam variáveis aleatórias contínuas, independentes e identicamente distribuídas, conforme a função de densidade dada por f(x) = 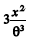 se 0 < x < 2, e f(x) = 0, se caso contrário, em que  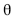> 0 é o parâmetro da distribuição.

Com base nas informações apresentadas no texto, assinale a opção incorreta.

• A.

  X ₁ = X ₂ = ... = X _n , mas a probabilidade P(X _i = X _j ), em que ij, é nula.

• B.
• C.
• D.

O P-valor do teste é superior a 2%.

• C. Certo
• E. Errado

Considere que uma amostra aleatória simples de n indivíduos a ser retirada de uma grande população seja representada por um vetor aleatório X^T = (X₁, X₂ , ..., X_n)^T, em que o índice sobrescrito T indica transposto. A média e o desvio padrão dessa população são iguais a •• e 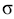, respectivamente. Considere também que U seja um vetor de dimensão n × 1 cujos elementos são todos unitários. Com base nessas informações, julgue os itens a seguir.

Se o vetor aleatório X segue uma distribuição normal multivariada, então a soma X_i + X_j, em que i > j, segue uma distribuição normal com média 2µ.

• C. Certo
• E. Errado

Considere que X₁, X₂, ..., X_n seja uma amostra aleatória simples de uma distribuição X, cuja função de densidade é dada por para para x < 0 ou x > 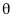 em que  > 0. Com base nessas informações, julgue os itens a seguir.

A média amostral 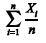 é o estimador de máxima verossimilhança para .

• C. Certo
• E. Errado