Questões de Estatística

 

A figura acima caracteriza a distribuição de uma variável aleatória X, em que f(x) representa a sua função de densidade e x, os seus valores possíveis. Considerando as informações acima, julgue os itens a seguir, referentes a probabilidade.

Considere a transformação Y = 4X + 3. Nessa situação, P (Y > 15) = P (Y < 4).

• C. Certo
• E. Errado

 

A figura acima caracteriza a distribuição de uma variável aleatória X, em que f(x) representa a sua função de densidade e x, os seus valores possíveis. Considerando as informações acima, julgue os itens a seguir, referentes a probabilidade.

• C. Certo
• E. Errado

A tabela abaixo apresenta os preços unitários ( p ) e as quantidades ( q ) de três utilidades no período de 2003 a 2004.

Por meio do método Agregativo Ponderado – Ano Base, conclui-se que de 2004 em relação a 2003 houve um aumento geral de:

• A. 40,82%
• B. 41,46%
• C. 36,36%.
• D. 77,55%

 

A figura acima caracteriza a distribuição de uma variável aleatória X, em que f(x) representa a sua função de densidade e x, os seus valores possíveis. Considerando as informações acima, julgue os itens a seguir, referentes a probabilidade.

• C. Certo
• E. Errado

Com base nessa situação hipotética, julgue os itens a seguir.

O desvio-padrão do custo de produção/componente pelo processo II é inferior a R$ 24,50.

• C. Certo
• E. Errado

Considere a distribuição conjunta abaixo de duas variáveis aleatórias discretas X e Y. Assinale a opção que dá o valor da covariância entre X e Y.

• A.

  –6,40

• B.

  –0,87

• C.

  –0,05

• D.

  0,00

• E.

  0,25

Com base nessa situação hipotética, julgue os itens a seguir.

Para que os dois processos forneçam distribuições de custos com o mesmo coeficiente de variação, o valor de a deve ser igual a R$ 50,00.

• C. Certo
• E. Errado

O enunciado seguinte diz respeito às questões 54 e 55.

O vetor Y=(Y1,Y2,Y3,Y4) tem distribuição normal multivariada com vetor de médias μ=(0,1,2,0) e matriz de  ariâncias-covariâncias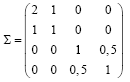

Assinale a opção correta.

• A.

  As variáveis aleatórias Y1 e Y2 são independentemente distribuídas.

• B.

  As variáveis aleatórias Y3 e Y4 são independentemente distribuídas.

• C.

  As variáveis aleatórias (Y1+Y3) e (Y2+Y4) não tem distribuição conjunta normal bivariada.

• D.

  Os vetores (Y1,Y2) e (Y3,Y4) são independentemente distribuídos.

• E.

  A variável aleatória Z=(Y1)2 + (Y2)2 tem distribuição qui-quadrado com 2 graus de liberdade.

• A.
• B.
• C.
• D.
• E. 0

Considere o processo AR(1) estacionário  com t ∈ Z(conjunto dos inteiros). A seqüência ε, é o ruído branco com variância unitária e φ = 0,5. Assinale a opção que dá o valor da função de autocovariância γ (h) do processo para h = 2.

• A.

  0,210

• B.

  0,333

• C.

  0,500

• D.

  1,000

• E.

  1,250