Questões de Estatística do ano 2006

A freqüência absoluta acumulada de um valor da variável é igual:

• A.

  à soma das freqüências absolutas anteriores.

• B.

  à soma das freqüências absolutas anteriores com a frequência absoluta desse valor.

• C.

  à diferença entre a freqüência total e o 1º quartil.

• D.

  às mudanças relativas na freqüência dos valores da variável.

• E.

  ao número total de observações.

Uma faculdade possui 2500 alunos dos quais 40% falam espanhol e 60% são do sexo masculino. Sabese que 25% das mulheres falam espanhol. Desse modo, o número de alunos do sexo masculino e que falam espanhol é igual a:

• a.

  500

• b.

  1100

• c.

  250

• d.

  750

• e.

  1750

No teste a seguir, elaborado com base em uma pesquisa internacional sobre auto-estima, o entrevistado deve marcar a opção que mais se aplica ao seu caso, em cada tópico. Considere que um entrevistado tenha assinalado as opções especificadas abaixo.

A partir dessas informações, julgue os itens seguintes.

Considere que um conjunto de empregados de uma empresa tenha respondido integralmente ao teste apresentado e tenha sido verificado que 15 deles fizeram uso da opção "às vezes", 9, da opção "raramente" e 13, da opção "sempre". Além disso, 4 desses empregados usaram as opções "às vezes" e "raramente", 8 usaram as opções "às vezes" e "sempre", 4 usaram as opções "raramente" e "sempre", e 3 usaram "às vezes", "sempre" e "raramente". Nessas situação, é correto afirmar que menos de 30 empregados dessa empresa responderam ao teste.

• C. Certo
• E. Errado

Considerando essas informações e os dados da tabela, disponível ao final das provas objetivas, de distribuição normal padrão, julgue os itens a seguir.

A estatística qui-quadrado do teste E é igual a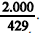

• C. Certo
• E. Errado

Considerando essas informações e os dados da tabela, disponível ao final das provas objetivas, de distribuição normal padrão, julgue os itens a seguir.

O teste qui-quadrado de homogeneidade (teste F) é equivalente aos testes C e E.

• C. Certo
• E. Errado

Texto para as questões de 56 a 58

Um estudo produziu a seguinte tabela de contingência, em que X e Y são duas variáveis binárias. Deseja-se testar a hipótese nula H₀: E(Y | X = x) = 0,20 + 0,55x, em que x é igual a 0 ou 1.

A estatística do teste qui-quadrado para o teste mencionado no texto é igual a

• A. 0,55.
• B. 1,10.
• C. 1,90.
• D. 2,21.

A opinião sobre o atendimento (entre bom, regular e ruim) aos pacientes em dois hospitais públicos foi estudado em duas cidades. Na cidade A sorteou-se 200 usuários e destes 50 classificaram em regular, 70 classificaram em ruim e os demais classificaram como bom o atendimento do hospital A . Na cidade B foram sorteados 200 usuários e 120 classificaram em bom, 50 classificaram em regular e os demais classificaram como ruim o atendimento do hospital B. Utilizou-se o teste qui-quadrado para avaliar se existe diferença no grau de satisfação com os hospitais das duas cidades. O valor observado do qui quadrado e a decisão do teste ao nível de 5% de significância são, respectivamente,

• A. 24, existe diferença significativa de opinião entre as cidades.
• B. 24, não existe diferença significativa de opinião entre as cidades.
• C. 25, existe diferença significativa de opinião entre as cidades.
• D. 26, existe diferença significativa de opinião entre as cidades.
• E. 26, não existe diferença significativa de opinião entre as cidades.

Para testar a aderência de conjunto de observações a uma densidade normal, os dados foram distribuídos em 10 classes e as freqüências observadas foram obtidas. As estimativas de máxima verossimilhança da média e da variância populacionais foram calculadas e seus valores foram usados para calcular as freqüências esperadas nas 10 classes. Em seguida, a estatística qui-quadrado usual foi calculada. Sob a hipótese nula de aderência, essa estatística tem distribuição qui-quadrado aproximada com o seguinte número de graus de liberdade:

• A. 6
• B. 7
• C. 8
• D. 9
• E. 10

Na análise da sinistralidade de uma determinada carteira, uma medida de discrepância existente entre as freqüências observadas e as esperadas é proporcionada pela estatística quí quadrado - X² . Com base nisso, pode-se afirmar que se:

• A. X² = 0, as freqüências teóricas (esperadas) e as observadas concordam exatamente.
• B. X² = 0, as freqüências teóricas (esperadas) e as observadas não concordam exatamente nem parcialmente.
• C. X² = 0, as freqüências teóricas (esperadas) e as observadas concordam parcialmente, pode ser aceita-se como tal.
• D. X² = 1, as freqüências teóricas(esperadas) e as observadas concordam exatamente.
• E. X² ¡Ù 0, as freqüências teóricas (esperadas) e as observadas concordam exatamente.

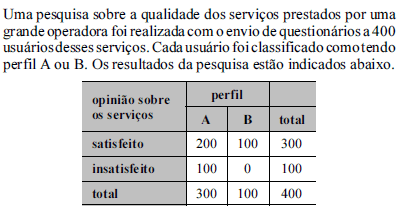
Com base nessas informações e com o auxílio da tabela da distribuição normal padrão, caso seja necessário, julgue os itens que se seguem.

A tabela de contingência apresenta uma freqüência observada menor do que 5, portanto o teste qui-quadrado para a avaliação da associação entre a opinião sobre os serviços e o perfil dos usuários não é recomendável.

• C. Certo
• E. Errado