Questões de Estatística do ano 2009
Lista completa de Questões de Estatística do ano 2009 para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Suponha que sejam realizados 10 ensaios independentes, cada um com dois resultados possíveis: sucesso e fracasso. Suponha que a probabilidade de sucesso em cada ensaio seja p. Desejando-se testar H0 : p = 0,4 contra H1 : p = 0,5, adotou-se {8, 9,10} como região crítica. A probabilidade de se cometer erro do tipo dois é
- A.

- B.

- C.

- D.

- E.

Instruções: Para responder às questões de números 32 a 34 utilize as informações a seguir.

Uma variável aleatória X tem distribuição normal com média μ e desvio padrão σ desconhecido. Desejando-se testar H0 : μ = 2 contra H1 : μ > 2 tomou-se uma amostra aleatória de 4 observações que forneceu os valores: 4, 2, 2 e 2. A um nível de significância de 10%, no teste mais poderoso, a hipótese H0 será rejeitada se a estatística média amostral X , apropriada ao teste, for maior ou igual a
- A.
2,819
- B.
2,767
- C.
2,673
- D.
2,541
- E.
2,520
O peso de pacotes de café é uma variável aleatória X : N (μ, σ2). Uma máquina de encher pacotes de café está regulada para fazê-lo com μ = 500 g e σ2 = 100 g2. Com o objetivo de manter sob controle a variabilidade do produto, a cada 30 minutos uma amostra aleatória de alguns pacotes é selecionada e testa-se se a variabilidade está controlada. Assim, desejando-se testar H0 : σ2 = 100 contra σ2 ≠ 100 toma-se uma amostra de n = 16 pacotes de café e observa-se para a variância amostral o valor 160 g2. O valor observado da estatística apropriada ao teste é
- A.
31
- B.
28
- C.
24
- D.
22
- E.
19
Um atributo X tem distribuição normal com média μ e variância populacional igual a 3.600. Uma amostra aleatória de tamanho 100 extraída da população, considerada de tamanho infinito, forneceu uma média de 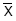 para X. Um teste estatístico é realizado sendo formuladas as hipóteses H0: μ = 200 (hipótese nula) contra H1: μ > 200 (hipótese alternativa). Sabe-se que H0 foi rejeitada a um nível de significância de 5%. Utilizando a informação da distribuição normal padrão (Z) em que a probabilidade
para X. Um teste estatístico é realizado sendo formuladas as hipóteses H0: μ = 200 (hipótese nula) contra H1: μ > 200 (hipótese alternativa). Sabe-se que H0 foi rejeitada a um nível de significância de 5%. Utilizando a informação da distribuição normal padrão (Z) em que a probabilidade 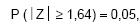 tem-se que o valor encontrado para
tem-se que o valor encontrado para 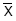 foi, no mínimo,
foi, no mínimo,
- A.
219,68
- B.
214,76
- C.
209,84
- D.
204,92
- E.
200,00
Um fabricante faz dois tipos de lâmpadas. Seja X a variável aleatória que representa o tempo de vida do primeiro tipo e Y a variável aleatória que representa o tempo de vida do segundo tipo. Sabe-se que X e Y são independentes e que os respectivos desvios padrões populacionais dos dois tipos são iguais a 250 horas, cada um. Um comprador testou 36 lâmpadas do tipo X e 64 lâmpadas do tipo Y, obtendo 1.000 horas e 1.200 horas de duração média para o tipo X e o tipo Y, respectivamente. Foram formuladas as seguintes hipóteses: H0: μx = μy (hipóteses nula, isto é, a vida média dos tipos X e Y é a mesma) e H1: μx ≠ μy (hipótese alternativa). Considerou-se para o teste que o tamanho das populações é infinito, além de serem normalmente distribuídas e que na distribuição normal padrão (Z) a probabilidade P (Z ≥ zα) = α (0 < α 0,5). Então, pode-se afirmar que a um nível de significância de 2 α
- A.
H0 não será rejeitada para zα = 3.
- B.
H0 será rejeitada para

- C.
H0 será rejeitada para

- D.
H0 não será rejeitada, para − 4 < zα < 4.
- E.
H0 será rejeitada para qualquer valor de
 devido aos valores obtidos pelas amostras.
devido aos valores obtidos pelas amostras.
Os lucros brutos anuais das empresas de um determinado ramo de atividade apresentam uma distribuição normal com média μ e variância populacional σ2 desconhecidas. A partir de uma amostra aleatória de tamanho 25 da população considerada de tamanho infinito, deseja-se testar a hipótese H0: μ = 20 milhões de reais contra a alternativa H1: μ > 20 milhões de reais, com a realização do teste t de Student. A média e o desvio padrão da amostra são iguais a 23 e 8, respectivamente, em milhões de reais. Seja tc o valor calculado correspondente para comparar com o valor tabelado tt da distribuição t de Student, com n graus de liberdade, ao nível de significância α. Então, é correto afirmar que
- A.
H0 não será rejeitada, ao nível de significância α, se tt > 1,875 com n = 24.
- B.
Se H0 foi rejeitada, ao nível de significância α, tem-se que tt > 9,375 com n = 24.
- C.
Se H0 foi rejeitada, ao nível de significância α, então para um nível de significância superior a α H0 não seria rejeitada.
- D.
1,875 < tc < 9,375 e n = 23.
- E.
tc = 9,375 e n = 23.
Com o objetivo de comprovar se dois grupos independentes diferem em tendências centrais, um analista utiliza a tabela abaixo formulando as hipóteses:
H0: Os 2 grupos provêm de populações com a mesma mediana (hipótese nula).
H1: A mediana de um grupo difere da mediana do outro grupo (hipótese alternativa).
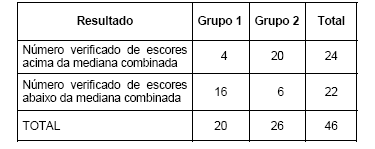
Então, é correto afirmar que
- A.
o teste da mediana não se aplica, uma vez que os tamanhos das respectivas amostras teriam que ser iguais.
- B.
o valor da mediana do estudo em questão corresponde à média aritmética do 23° e 24° elementos, combinando os escores dos dois grupos.
- C.
para aplicação do teste da mediana há a necessidade, primeiramente, de se conhecer a distribuição da população.
- D.
combinando os escores dos dois grupos, há a necessidade de verificar se o valor da mediana do conjunto formado pertence a este conjunto. Caso contrário, o teste da mediana não deve ser aplicado.
- E.
caso seja aplicado o teste da mediana, devido à soma dos tamanhos das duas amostras, utiliza-se o qui-quadrado com correção de continuidade.
Considere um teste estatístico envolvendo uma população normalmente distribuída em que se deseja testar, com relação a um parâmetro da distribuição, a hipótese nula (H0) contra a hipótese alternativa (H1), ao nível de significância α. Seja β a probabilidade de aceitar H0 quando H0 for falsa. Então,
- A.
β corresponde ao erro tipo I ou erro de primeira espécie.
- B.
α > β.
- C.
α = 1− β.
- D.
a região crítica do teste é determinada em função de β.
- E.
 corresponde à probabilidade de rejeitar H0 quando H0 for verdadeira.
corresponde à probabilidade de rejeitar H0 quando H0 for verdadeira.
Uma experiência consiste em verificar se uma moeda é honesta. Em 10 lançamentos da moeda, decide-se pela honestidade da moeda se o número de caras (n) for tal que 4 ≤ n ≤ 6 . A probabilidade de rejeitar a hipótese da moeda ser honesta, quando ela for correta é
- A.

- B.

- C.

- D.

- E.

Em uma cidade é realizada uma pesquisa sobre a preferência dos eleitores com relação a um determinado candidato, que afirma ter 60% da preferência. Uma amostra aleatória de tamanho 600 foi extraída da população, considerada de tamanho infinito, sendo que 330 eleitores manifestaram sua preferência pelo candidato. Com base nesta amostra, deseja-se testar a hipótese H0 : p = 60% (hipótese nula) contra H1 : p ≠ 60% (hipótese alternativa), em que p é a proporção dos eleitores que têm preferência pelo candidato. Para a análise considerou-se normal a distribuição amostral da frequência relativa dos eleitores que têm preferência pelo candidato e que na distribuição normal padrão Z a probabilidade P(|Z| ≤ 1,96) = 95% e P(|Z| ≤ 2,58) = 99%. A conclusão é que H0
- A.
não é rejeitada tanto ao nível de significância de 1% como ao nível de significância de 5%.
- B.
é rejeitada ao nível de significância de 5%.
- C.
é rejeitada ao nível de significância de 1%.
- D.
não é rejeitada para algum nível de significância superior a 5%.
- E.
é rejeitada para algum nível de significância inferior a 1%.


