Questões de Estatística do ano 2013

• A.

  O desvio padrão amostral foi inferior a 30 minutos.

• B.

  A amplitude total, que representa a diferença entre as observações nas extremidades do conjunto de dados, foi igual a 30 minutos.

• C.

  O desvio médio absoluto em torno da média amostral foi superior a 25 minutos.

• D.

  A variância amostral desse conjunto de dados foi inferior a 600 minutos².

• E.

  O coeficiente de variação, que representa a amplitude entre o quartil superior e o inferior, foi igual a 80 minutos.

Considere que a probabilidade de haver inconsistência em uma declaração do imposto de renda seja igual a 0,10 e que X represente o total de declarações inconsistentes em uma amostra aleatória simples de 3.600 declarações. Com base nessas informações, assinale a opção correta.

• A.

  A variância de X é superior a 350.

• B.

  A moda da distribuição X é igual ou superior a 3.000.

• C.

  O desvio padrão da quantidade X é igual a 18.

• D.

  A mediana da distribuição de X é superior a 500.

• E.

  O total esperado de declarações inconsistentes na amostra é superior a 500.

• A.

  A fração amostral no estrato 2 é superior à fração amostral no estrato 1.

• B.

  Com respeito ao tamanho da amostra retirada de cada estrato, o plano amostral apresentado considera a alocação ótima de Neyman.

• C.

  Na amostragem em tela, retira-se uma amostra aleatória simples de cada estrato.

• D.

  O objetivo da estratificação é formar subgrupos heterogêneos, de modo a maximizar o desvio padrão da variável de interesse em cada estrato.

• E.

  No plano amostral apresentado, para o cálculo da estimativa da média populacional, é necessário utilizar um fator de expansão para corrigir os vícios na estimação provocados pela estratificação.

Um levantamento estatístico foi realizado com o objetivo de estimar o percentual populacional (π) de usuários satisfeitos com os serviços de transporte público de uma cidade. De um grupo de 400 usuários selecionados por amostragem aleatória simples, 320 se mostraram satisfeitos com esses serviços. Considerando que P(|Z|<2) = 0,9545, em que Z representa a distribuição normal padrão, assinale a opção correspondente ao intervalo de 95,45% de confiança do percentual.

• A.

  80% ± 8%

• B.

  80% ± 10%

• C.

  80% ± 20%

• D.

  80% ± 2%

• E.

  80% ± 4%

Em uma propaganda, um fabricante afirma que os pneus produzidos por ele duram, em média, 50.000 km. Para testar essa afirmação, uma agência de fiscalização selecionou uma amostra aleatória de 36 pneus produzidos pelo fabricante. Nessa amostra, observou-se uma duração média de 48.000 km e desvio padrão amostral de 2.000 km. Considerando as hipóteses H₀: μ = 50.000 km e H₁: μ < 50.000 km e que a durabilidade do pneu segue uma distribuição normal, assinale a opção correta.

• A.

  O nível descritivo de um teste, também conhecido como p-valor, representa a probabilidade de se decidir pela aceitação da hipótese nula, dado que ela é verdadeira.

• B.

  O erro do tipo I, ou nível de significância do teste, representa o risco probabilístico de se decidir pela aceitação da hipótese nula, dado que ela é falsa.

• C.

  No teste de hipóteses, controla-se, em geral, o erro do tipo II, também conhecido como poder do teste.

• D.

  A estatística do teste t de Student é igual a 6.

• E.

  O p-valor do teste é igual a P(T < -6), em que T representa a distribuição t de Student com 35 graus de liberdade.

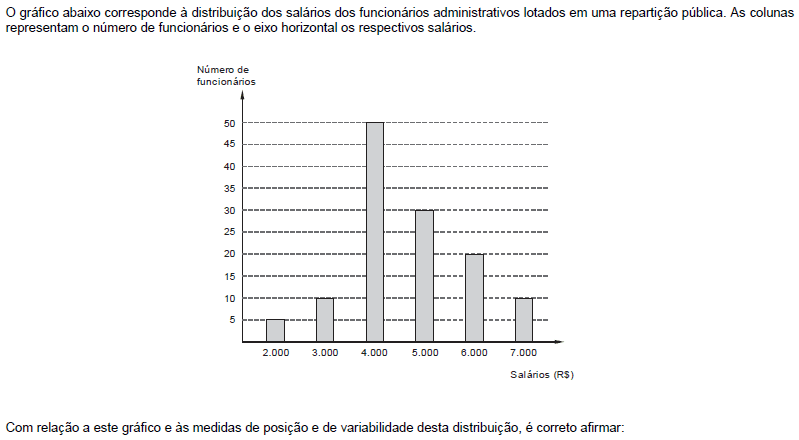
• A.

  Os valores da média aritmética, da mediana e da moda dos salários dos funcionários são iguais.

• B.

  60% dos funcionários ganham acima do valor da moda.

• C.

  15% dos funcionários ganham menos que o valor da mediana.

• D.

  Concedendo um abono fixo no valor de R$ 500,00 para todos os empregados, a correspondente nova média aritmética fica aumentada de R$ 500,00 e a nova variância permanece inalterada.

• E.

  Concedendo um reajuste de 10% a todos os funcionários, a correspondente nova média aritmética fica multiplicada por 1,10 e o novo desvio padrão fica multiplicado por 1,21.

O número de processos com uma determinada característica autuados por dia em um órgão público é considerado como uma variável aleatória X com distribuição de Poisson com média λ. Considere que P(X = 2) = 3 . P(X = 4), e⁻¹ = 0,37, e⁻² = 0,14, e⁻³ = 0,05 e e⁻⁴ = 0,02, em que P(X = k) é a probabilidade de X ser igual a k e e a base dos logaritmos neperianos. A probabilidade de que pelo menos 2 processos sejam autuados em um determinado dia é igual a

• A.

  95%.

• B.

  90%.

• C.

  80%.

• D.

  63%.

• E.

  58%.

• A.

  R$ 3.592,20.

• B.

  R$ 3.444,00.

• C.

  R$ 3.342,00.

• D.

  R$ 3.332,00.

• E.

  R$ 3.264,00.

Uma população, considerada de tamanho infinito, formada pelas alturas dos habitantes de uma cidade é normalmente distribuída com média μ e variância populacional igual a 225 cm². Deseja-se saber, a um determinado nível de significância, se a altura média dos habitantes da cidade é superior a 170 cm com a formulação das hipóteses H₀: μ = 170 cm (hipótese nula) e H₁: μ > 170 cm (hipótese alternativa). Uma amostra aleatória de tamanho 400 é extraída desta população, obtendo-se uma média amostral igual a 171,5 cm. Considere que na distribuição normal padrão (Z) as probabilidades P(Z > 1,64) = 0,05 e P(Z > 2,33) = 0,01. Com base nesta amostra, tem-se que a hipótese H₀

• A.

  não é rejeitada ao nível de significância de 1% e é rejeitada ao nível de 5%.

• B.

  é rejeitada ao nível de significância de 1%, mas não ao nível de 5%.

• C.

  é rejeitada tanto ao nível de significância de 1% como ao nível de 5%.

• D.

  é rejeitada para qualquer nível de significância inferior a 1%.

• E.

  não é rejeitada para qualquer nível de significância superior a 5%.

Em um estudo envolvendo 20 pares de observações (X_i , Y_i), i = 1, 2, 3, ... , 20, foi observada a existência de uma correlação entre as variáveis X e Y. Desejando-se obter uma relação entre X e Y optou-se pelo modelo linear Y_i = α + βXi + ε_i , em que i é a i-ésima observação, α e β são parâmetros desconhecidos e εi o erro aleatório, com as respectivas hipóteses consideradas para a regressão linear simples. Utilizou-se o método dos mínimos quadrados para obter as estimativas de α e β e as médias encontradas para as observações X_i e Y_i foram 20 e 50, respectivamente. Se a reta, cuja equação foi encontrada pelo método dos mínimos quadrados, passa pelo ponto (35 , 80), então, considerando esta equação, tem-se que

• A.

  o menor valor inteiro encontrado para X, tal que Y > 100, é igual a 46.

• B.

  a previsão de Y para X = 25 é igual a 65.

• C.

  o valor da estimativa encontrado para α é igual a 20.

• D.

  o valor de X, tal que a previsão para Y é igual a 40, é igual a 20.

• E.

  o acréscimo verificado para Y, quando X aumenta de uma unidade, é igual a 10.