Questões sobre Conceitos de Estatística

Karla mora perto de dois supermercados (Compre Bem e Compre Fácil) e costuma fazer compras semanalmente, sempre em busca de promoções que são oferecidas pelos dois estabelecimentos. O esquema seguinte mostra a probabilidade de Karla comprar no dia seguinte em cada um desses supermercados.

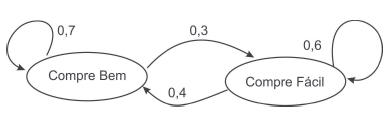
Se a probabilidade de que Karla vá ao supermercado Compre Bem hoje é de 20%, a probabilidade incondicional de ela voltar a esse mercado amanhã é de

• A.

  0,06.

• B.

  0,14.

• C.

  0,46.

• D.

  0,49.

• E.

  0,70.

Texto IV, para responder às questões de 49 a 51.

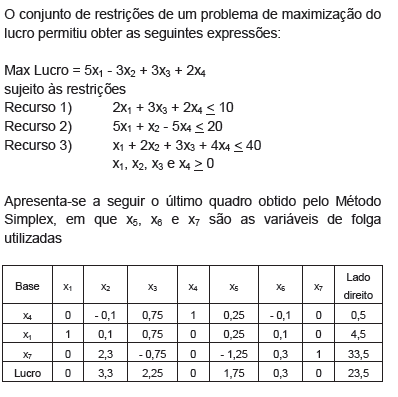
Com relação à solução apontada pela tabela, é correto afirmar que há sobra do(s) recurso(s)

• A.

  1.

• B.

  2.

• C.

  3.

• D.

  1 e 2.

• E.

  1 e 3.

Texto IV, para responder às questões de 49 a 51.

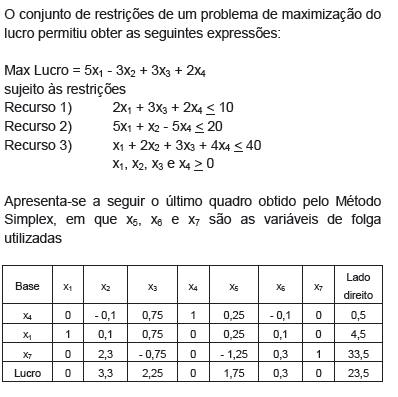
O valor máximo que pode ser dado ao coeficiente de x3 na função-objetivo, para que a solução encontrada no quadro acima continue a ser a solução ótima, é

• A.

  3,75.

• B.

  5,25.

• C.

  8,25.

• D.

  11,25.

• E.

  24,75.

Texto IV, para responder às questões de 49 a 51.

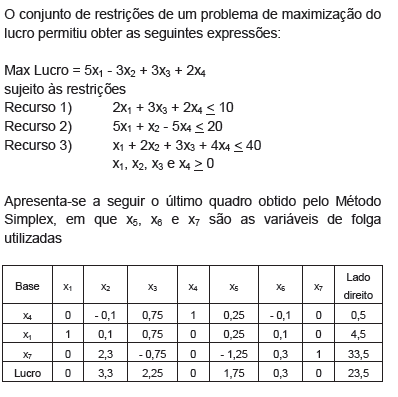
De quanto o lucro aumentaria, caso fosse possível dispor de mais 1 unidade do recurso 2?

• A.

  0

• B.

  0,30

• C.

  1,75

• D.

  2,25

• E.

  3,30

As ocorrências diárias de situações de emergência em uma instalação industrial são aleatórias e usualmente consideradas independentes umas das outras. Dessa forma, o modelo mais adequado para a simulação dos instantes de ocorrências é a Distribuição de Poisson e, consequentemente, os intervalos entre as ocorrências obedecem à Distribuição Exponencial. Na prática, observa-se que o tempo dedicado por um engenheiro à solução de cada emergência é bem modelado também pela Distribuição Exponencial. Esses são alguns dos motivos para que, em simulação desses processos de atendimento, o tempo (T) entre ocorrências e o tempo (T) de tratamento das mesmas sejam modelados por Distribuições Exponenciais que, entre outros aspectos, têm a propriedade denominada “ausência de memória” que (para quaisquer t > 0 e a > 0) é traduzida por:

• A. P(T > t + a | T > a) = P(T > t)
• B.
• C.
• D. P(0 < T < a) > P(t < T < t + a)
• E. P(0 < T < a) = P(t < T < t + a)

As técnicas de simulação são muito importantes em uma grande variedade de projetos quando estes apresentam cálculos muito complexos ou experimentos reais muito dispendiosos. Na base da simulação, tem-se a necessidade de geração de números pseudoaleatórios, quando as duas principais preocupações são: (1) um possível número deve ter a mesma probabilidade de ocorrer que qualquer outro dentre os demais possíveis números e (2) deve existir independência entre as ocorrências, isto é, a probabilidade de ocorrência de um número não deve ser afetada pelas eventuais ocorrências dos demais possíveis números. Os métodos de geração mais adotados na prática são: congruência mista (mixed congruential method), congruência multiplicativa (multiplicative congruential method) e congruência aditiva (additive congruential method). Considere os números inteiros K, L, M e N, tais que: 0 < K < M; 0 < L < M e N = 1, 2, 3... Para serem gerados números pseudoaleatórios entre 0 e M-1, iniciase com uma semente X₀ aleatoriamente escolhida e adota- se a relação de recorrência XN+1 = f(X_N, X_N-1, K, L)(módulo M), isto é, X_N+1 é o resto da divisão de f(X_N, X_N-1, K, L) por M. Nessas condições, quando

• A. f(XN, XN-1, K, L) = K.XN + L, tem-se a congruência mista.
• B. f(XN, XN-1, K, L) = K.XN / L, tem-se a congruência mista.
• C. f(XN, XN-1, K, L) = K.(XN + L), tem-se a congruência multiplicativa.
• D. f(XN, XN-1, K, L) = K.XN + L.XN-1, tem-se a congruência mista.
• E. f(XN, XN-1, K, L) = K.XN.XN-1, + L, tem-se a congruência multiplicativa.

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Com base nessas informações, julgue os itens subsequentes.

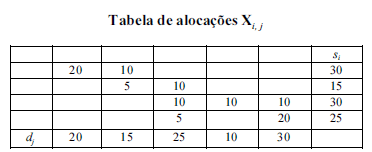
Considere que m = 4, n = 5 e que as ofertas e demandas sejam, respectivamente, (s₁, s₂, s₃, s₄, s₅) = (20, 15, 25, 10, 30) e (d₁, d₂, d₃, d₄) = (30, 15, 30, 25). Nesse caso, é correto afirmar que uma solução básica inicial pode ser determinada pela regra do ponto extremo noroeste, que determina as alocações iniciais indicadas, conforme a seguinte tabela simplex de transporte.

• C. Certo
• E. Errado

A distância de Mahalanobis é útil para análise de clusters e detecção de valores atípicos (outliers).

• C. Certo
• E. Errado

Julgue os itens subsequentes, relativos a planejamento fatorial.

Em um planejamento fatorial fracionário, o estimador da média global é viciado.

• C. Certo
• E. Errado