Questões sobre Conceitos de Estatística

Observe as afirmações:

I. O termo Estatística provém da palavra Estado e foi utilizado originalmente para denominar levantamentos de dados, cuja finalidade era orientar o Estado em suas decisões.

II. A Estatística Descritiva é a parte da Estatística que tem por objetivo obter e generalizar conclusões para a população a partir de uma amostra, através do cálculo de probabilidade.

III. A coleta , a organização e a descrição dos dados estão a cargo da Estatística Indutiva ou Inferencial.

Pode-se dizer que:

• A.

  Todas estão incorretas

• B.

  Todas estão corretas.

• C.

  Apenas I está correta.

• D.

  Apenas II está correta.

• E.

  Apenas III está correta.

Observe as afirmações:

I. O termo Estatística provém da palavra Estado e foi utilizado originalmente para denominar levantamentos de dados, cuja finalidade era orientar o Estado em suas decisões.

II. A Estatística Descritiva é a parte da Estatística que tem por objetivo obter e generalizar conclusões para a população a partir de uma amostra, através do cálculo de probabilidade.

III. A coleta , a organização e a descrição dos dados estão a cargo da Estatística Indutiva ou Inferencial.

Pode-se dizer que:

• A.

  Todas estão incorretas.

• B.

  Todas estão corretas.

• C.

  Apenas I está correta.

• D.

  Apenas II está correta.

• E.

  Apenas III está correta.

Na estimativa das reservas de petróleo, podem ser empregados métodos probabilísticos e determinísticos. Os métodos probabilísticos baseiam-se na utilização de faixas e diferentes graus de certeza para cada um dos parâmetros envolvidos no cálculo dessas reservas.

De acordo com o estabelecido pela Agência Nacional de Petróleo, a abordagem probabilística deve utilizar uma probabilidade de 90% para as reservas

• A. provadas, 50% para as reservas provadas mais reservas possíveis e 10% para as reservas provadas mais reservas prováveis mais reservas possíveis.
• B. provadas, 50% para as reservas provadas mais reservas prováveis e 10% para as reservas provadas mais reservas prováveis mais reservas possíveis.
• C. provadas, 50% para as reservas provadas mais reservas prováveis e 10% para as reservas provadas mais reservas possíveis.
• D. prováveis, 50% para as reservas provadas mais reservas possíveis e 10% para as reservas provadas mais reservas prováveis mais reservas possíveis.
• E. prováveis, 50% para as reservas prováveis mais reservas possíveis e 10% para as reservas provadas mais reservas prováveis mais reservas possíveis.

Considere um estimador T de um parâmetro θ de uma população. Se E(T) = θ, então T é um estimador

• A.

  não viesado.

• B.

  viesado.

• C.

  consistente.

• D.

  tendencioso.

• E.

  eficiente.

Ensaios em laboratório, tendo probabilidade θ (desconhecida) de sucesso em cada tentativa, são realizados sucessiva e independentemente até a ocorrência do primeiro sucesso. Para cada realização experimental, seja X a variável aleatória que representa o número de ensaios realizados até a ocorrência do primeiro sucesso.

Se quatro realizações são feitas em laboratório, obtendo-se a amostra {3, 3, 4, 5}, o estimador de máxima verossimilhança para θ, à luz dessa amostra, é dado por

• A. 1/3
• B. 1/5
• C. 1/15
• D. 4/15
• E. 47/60

Considere uma amostra aleatória (X, Y, Z), com reposição, extraída de uma população normal com média μ e variância 1. Considere também os 3 estimadores não viesados de μ , com m, n e p sendo parâmetros reais:

E₁ = mX − 2nY − pZ

E₂ = 2mX + nY − 4pZ

E₃ = mX − 8nY + pZ

Entre os 3 estimadores, o mais eficiente apresenta uma variância igual a

• A.

  27.

• B.

  36.

• C.

  42.

• D.

  45.

• E.

  49.

• A.

  0,20.

• B.

  0,22.

• C.

  0,25.

• D.

  0,44.

• E.

  0,50.

Deseja-se obter uma estimativa pontual do parâmetro p da distribuição geométrica P(X = x) = (1 − p)^{x − 1}p (x = 1, 2, 3, . . . ) sabendo-se que o acontecimento cuja probabilidade é p ocorreu em 5 experiências, pela primeira vez na primeira, terceira, segunda, quarta e segunda, respectivamente. Utilizando o método dos momentos, encontra-se que o valor desta estimativa é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Seja o modelo linear de análise de covariância Y_i = α + βD_i + γX_i + ε_i referente a um determinado ramo de atividade. Y_i representa o salário anual de um empregado i, X_i é o número de anos de experiência do empregado i e ε_i é o erro aleatório com as respectivas hipóteses da correspondente regressão (α, β e γ são parâmetros desconhecidos). Com relação a este modelo, dado que D_i = 1 se o empregado i for homem e D_i = 0 se o empregado i for mulher, pode-se afirmar que

• A.

  o salário anual de um empregado do sexo feminino nunca é igual ao salário anual de um empregado do sexo masculino.

• B.

  a função do salário anual de um empregado do sexo masculino apresenta um intercepto igual a (β + γ).

• C. o módulo da diferença entre o salário anual de um homem e o salário anual de uma mulher, com o mesmo número de anos de experiência, é igual a |β |.
• D.

  as funções salários anuais de empregados homens e empregados mulheres, em relação aos anos de experiência, têm inclinações diferentes.

• E.

  as funções salários anuais de empregados homens e empregados mulheres, em relação aos anos de experiência, apresentam o mesmo intercepto.

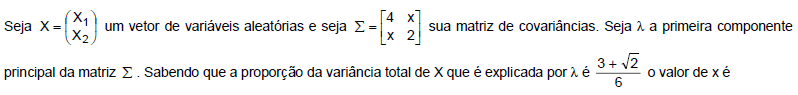
• A.

  0,25 ou −0,25.

• B.

  0,5 ou −0,5.

• C.

  0,75 ou −0,75.

• D.

  1 ou −1.

• E.