Questões sobre Correlação

           Em 2006, o rendimento do trabalhador com emprego formal somou R$ 43,5 bilhões, elevando o consumo e, conseqüentemente, a contratação de pessoal. Puxada pelo volume recorde de empregos formais e pela valorização dos rendimentos dos trabalhadores, a massa salarial registrou o maior crescimento desde 1995. De 2005 para 2006, a expansão chegou a 11,96%, atingindo o montante de R$ 43,5 bilhões. Esse aumento mostra que os brasileiros estão com mais dinheiro no bolso e, conseqüentemente, vão às compras. Para atender o ímpeto consumista, as empresas investem mais em produção, o que se reflete na contratação de novos trabalhadores. Tanto é que, em 2006, foram criados quase 1,917 milhão de empregos formais — o melhor resultado da série histórica da RAIS (relação anual de informações sociais), iniciada em 1985 —, um acréscimo de 5,77% em comparação a 2005. O setor de serviços foi o que mais contribuiu para a alta do emprego em 2006, com a abertura de 719,1 mil novas vagas. Em segundo lugar aparece a indústria de transformação (461,3 mil), seguida pelo comércio (325,2 mil) e administração pública (177,9 mil). A figura a seguir mostra alguns dados relevantes acerca da renda e da oportunidade de emprego do trabalhador brasileiro.

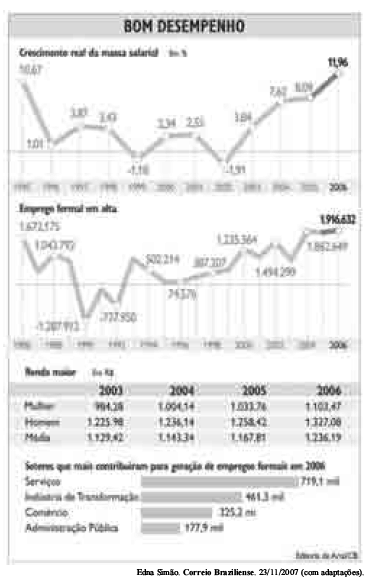
Considerando as informações ao lado, julgue os itens a seguir.

 

Se o gênero for representado por uma variável binária Y que assume valor 0 para o caso masculino e valor 1 para o feminino, então a renda e Y serão positivamente correlacionadas.

• C. Certo
• E. Errado

       Um estudo sobre a segmentação do mercado de trabalho comparou o salário daquele que trabalha por conta própria (Y, em R$ mil) com o salário daquele que tem a carteira assinada (X, em R$ mil). Foi ajustado um modelo de regressão linear na forma Y = ax + b + g, em que a e b são os coeficientes do modelo e g representa um erro aleatório com média zero e desvio-padrão 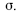 As estimativas de mínimos quadrados ordinários para os coeficientes a e b foram respectivamente iguais a 0,5 e R$ 6 mil. A quantidade de observações utilizadas para o ajuste do modelo foi igual a 400, e os desvios-padrão amostrais de Y e X foram, respectivamente, iguais a R$ 2 mil e R$ 1,5 mil.

Com base nessas informações, julgue os itens subseqüentes.

A correlação linear de Pearson entre Y e X é inferior a 0,45.

• C. Certo
• E. Errado

A partir dessas informações, julgue os itens seguintes.

A rotatividade da mão-de-obra e a oferta de emprego são variáveis positivamente correlacionadas.

• C. Certo
• E. Errado

A partir dessas informações, julgue os itens seguintes.

A correlação parcial entre X₁ e X₃ é inferior a 0,40.

• C. Certo
• E. Errado

Considere que um processo estocástico de Wiener seja representado por 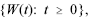 com Var[W(t)] = 0,25t e a transformação X(t) = [W(t)]². Nessa situação, julgue os itens que se seguem.

A correlação linear entre W(t) - W(t-1) e W(t +2)- W(t +1) é superior a 0,1.

• C. Certo
• E. Errado

A partir das informações acima, julgue os itens subseqüentes.

A correlação linear entre as despesas de 2006 e 2007, observada na pesquisa, é superior a 0,8.

• C. Certo
• E. Errado

O Coeficiente de Correlação Linear de Pearson entre os desempenhos de determinados alunos em duas avaliações nacionais é igual a 0,844. Nesse caso, conclui-se que a proporção da variabilidade nos resultados de uma das avaliações explicada pela relação linear entre elas é

• A.

  15,6%

• B.

  39,4%

• C.

  71,2%

• D.

  84,4%

• E.

  91,8%

Analisando-se os gráficos, foram feitas as informações a seguir.

I - Mais de 50,0% da variação em Y é explicada pela relação linear entre Y e a variável X ₂.

II - A relação linear entre Y e a variável X ₃ explica 53,2% da variação em Y.

III - A variação de uma unidade em X ₃ provoca um aumento de 8,69 unidades em Y.

IV - O coeficiente de correlação linear entre as variáveis Y e X ₃ é maior do que entre Y e X ₂.

Estão corretas APENAS as afirmações

• A.

  I e IV

• B.

  II e III

• C.

  II e IV

• D.

  I, II e III

• E.

  II, III e IV

As questões de n^os 57 a 59 referem-se aos resultados de um teste de associação entre as variáveis representadas na tabela de contingência a seguir.

O valor da estatística qui-quadrado e o nível descritivo do teste (p-value) observados foram, respectivamente, X ²=1,811 e 0,770.

O Coeficiente de Contingência de Pearson é

• A.
• B.
• C.
• D.
• E.

Considere as asserções a seguir.

O Coeficiente de Correlação Linear de Pearson é necessariamente um número no intervalo (−1 , 1).

PORQUE

O Coeficiente de Correlação Linear de Pearson só pode ser calculado para variáveis quantitativas.

Analisando-se as asserções, conclui-se que

• A.

  as duas asserções são verdadeiras, e a segunda é uma justificativa correta da primeira.

• B.

  as duas asserções são verdadeiras, e a segunda não é uma justificativa correta da primeira.

• C.

  a primeira asserção é verdadeira, e a segunda é falsa.

• D.

  a primeira asserção é falsa, e a segunda é verdadeira.

• E.

  a primeira e a segunda asserções são falsas.