Questões sobre Geral

Suponha que um empresário precise estimar o tempo médio de atendimento em seu restaurante. De uma amostra aleatória de 400 atendimentos, ele observa que a média amostral dos tempos é igual a 1,2 minuto com desvio padrão amostral de 0,8 minuto. A partir de um teste estatístico, esse empresário conclui que a distribuição do tempo de atendimento segue uma distribuição aproximadamente Normal.

 Considerando que Φ(1,96) = 0,975, em que Φ(z) representa a função de distribuição acumulada da distribuição Normal padrão, e com base nas informações apresentadas acima, julgue os itens a seguir.

Com 95% de confiança, a estimativa intervalar para o tempo médio de atendimento é [1,1216 minuto; 1,2784 minuto].

• C. Certo
• E. Errado

Suponha que um empresário precise estimar o tempo médio de atendimento em seu restaurante. De uma amostra aleatória de 400 atendimentos, ele observa que a média amostral dos tempos é igual a 1,2 minuto com desvio padrão amostral de 0,8 minuto. A partir de um teste estatístico, esse empresário conclui que a distribuição do tempo de atendimento segue uma distribuição aproximadamente Normal.

 Considerando que Φ(1,96) = 0,975, em que Φ(z) representa a função de distribuição acumulada da distribuição Normal padrão, e com base nas informações apresentadas acima, julgue os itens a seguir.

Considere o teste de hipóteses Ho: µ 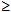 1,3 minuto versus H1: µ < 1,3 minuto, em que µ representa o tempo médio populacional de atendimento, Ho é a hipótese nula e H1 é a hipótese alternativa. Nessa situação, fixando-se o nível de significância em 2,5%, verificam-se evidências estatisticamente fortes para que a hipótese nula seja rejeitada.

• C. Certo
• E. Errado

Suponha que um empresário precise estimar o tempo médio de atendimento em seu restaurante. De uma amostra aleatória de 400 atendimentos, ele observa que a média amostral dos tempos é igual a 1,2 minuto com desvio padrão amostral de 0,8 minuto. A partir de um teste estatístico, esse empresário conclui que a distribuição do tempo de atendimento segue uma distribuição aproximadamente Normal.

 Considerando que Φ(1,96) = 0,975, em que Φ(z) representa a função de distribuição acumulada da distribuição Normal padrão, e com base nas informações apresentadas acima, julgue os itens a seguir.

A estatística de Shapiro-Wilk é uma medida apropriada que permite testar se a distribuição do tempo de atendimento segue uma distribuição aproximadamente Normal.

• C. Certo
• E. Errado

Um experimento foi realizado com o propósito de avaliar se a produtividade dos operários de uma indústria depende do método de treinamento. Para isso, vinte operários inexperientes foram selecionados aleatoriamente, sendo dez deles treinados pelo método A e os outros dez pelo método B. Após o treinamento, esses operários ingressaram na linha de produção, e seus índices de produtividade foram calculados. Constatou-se que a produtividade média e o desvio padrão amostral da produtividade dos dez operários treinados pelo método A foram iguais a 8 e 5, respectivamente. Daqueles que foram treinados pelo método B, a média e o desvio padrão amostral da produtividade foram iguais a 7 e 4, respectivamente.

 Em face dessa situação hipotética e considerando que os índices de produtividade tenham seguido distribuições Normais, julgue os itens que se seguem.

Se os índices de produtividade relativos aos métodos A e B são amostras de duas populações independentes com variâncias diferentes, então a estimativa da variância da diferença entre as médias amostrais relativas aos métodos A e B é superior a 16 e é inferior a 25.

• C. Certo
• E. Errado

Um experimento foi realizado com o propósito de avaliar se a produtividade dos operários de uma indústria depende do método de treinamento. Para isso, vinte operários inexperientes foram selecionados aleatoriamente, sendo dez deles treinados pelo método A e os outros dez pelo método B. Após o treinamento, esses operários ingressaram na linha de produção, e seus índices de produtividade foram calculados. Constatou-se que a produtividade média e o desvio padrão amostral da produtividade dos dez operários treinados pelo método A foram iguais a 8 e 5, respectivamente. Daqueles que foram treinados pelo método B, a média e o desvio padrão amostral da produtividade foram iguais a 7 e 4, respectivamente.

 Em face dessa situação hipotética e considerando que os índices de produtividade tenham seguido distribuições Normais, julgue os itens que se seguem.

Caso seja utilizado — para testar se o índice médio de produtividade independe do método de treinamento A e B — um teste t com a suposição de que as variâncias populacionais tenham sido iguais, então, o quadrado da razão t será superior a 3.

• C. Certo
• E. Errado

Um experimento foi realizado com o propósito de avaliar se a produtividade dos operários de uma indústria depende do método de treinamento. Para isso, vinte operários inexperientes foram selecionados aleatoriamente, sendo dez deles treinados pelo método A e os outros dez pelo método B. Após o treinamento, esses operários ingressaram na linha de produção, e seus índices de produtividade foram calculados. Constatou-se que a produtividade média e o desvio padrão amostral da produtividade dos dez operários treinados pelo método A foram iguais a 8 e 5, respectivamente. Daqueles que foram treinados pelo método B, a média e o desvio padrão amostral da produtividade foram iguais a 7 e 4, respectivamente.

 Em face dessa situação hipotética e considerando que os índices de produtividade tenham seguido distribuições Normais, julgue os itens que se seguem.

Na situação apresentada, descreve-se um experimento com dados emparelhados.

• C. Certo
• E. Errado

Um experimento foi realizado com o propósito de avaliar se a produtividade dos operários de uma indústria depende do método de treinamento. Para isso, vinte operários inexperientes foram selecionados aleatoriamente, sendo dez deles treinados pelo método A e os outros dez pelo método B. Após o treinamento, esses operários ingressaram na linha de produção, e seus índices de produtividade foram calculados. Constatou-se que a produtividade média e o desvio padrão amostral da produtividade dos dez operários treinados pelo método A foram iguais a 8 e 5, respectivamente. Daqueles que foram treinados pelo método B, a média e o desvio padrão amostral da produtividade foram iguais a 7 e 4, respectivamente.

 Em face dessa situação hipotética e considerando que os índices de produtividade tenham seguido distribuições Normais, julgue os itens que se seguem.

De acordo com o teste t, para testar se a média dos índices de produtividade daqueles que foram treinados pelo método A foi estatisticamente igual à média dos índices de produtividade daqueles que foram treinados pelo método B, o número de graus de liberdade a ser considerado é inferior a 8.

• C. Certo
• E. Errado

Um experimento foi realizado com o propósito de avaliar se a produtividade dos operários de uma indústria depende do método de treinamento. Para isso, vinte operários inexperientes foram selecionados aleatoriamente, sendo dez deles treinados pelo método A e os outros dez pelo método B. Após o treinamento, esses operários ingressaram na linha de produção, e seus índices de produtividade foram calculados. Constatou-se que a produtividade média e o desvio padrão amostral da produtividade dos dez operários treinados pelo método A foram iguais a 8 e 5, respectivamente. Daqueles que foram treinados pelo método B, a média e o desvio padrão amostral da produtividade foram iguais a 7 e 4, respectivamente.

 Em face dessa situação hipotética e considerando que os índices de produtividade tenham seguido distribuições Normais, julgue os itens que se seguem.

Ao testar se as variâncias das distribuições são iguais ou não, a estatística do teste F será superior a 0,5 e será inferior a 1,7.

• C. Certo
• E. Errado

Uma empresa possui dois fornecedores, A e B, de determinada matéria-prima. No ato do recebimento dessa matéria, é feita uma inspeção de qualidade. Como resultado, cada lote recebido é classificado como 0 = inaceitável ou 1 = aceitável. Depois de receber 110 lotes do fornecedor A e 90 lotes do fornecedor B, os resultados foram os seguintes:

Com base nas informações apresentadas acima, julgue os itens
seguintes.

É inferior a 1 a estatística do teste χ2 de independência na tabela de contingência.

• C. Certo
• E. Errado

Uma empresa possui dois fornecedores, A e B, de determinada matéria-prima. No ato do recebimento dessa matéria, é feita uma inspeção de qualidade. Como resultado, cada lote recebido é classificado como 0 = inaceitável ou 1 = aceitável. Depois de receber 110 lotes do fornecedor A e 90 lotes do fornecedor B, os resultados foram os seguintes:

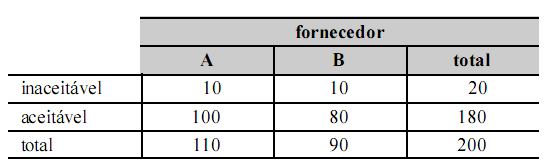
Com base nas informações apresentadas acima, julgue os itens
seguintes.

O valor do coeficiente de contingência é superior a 1,4 e é inferior a 1,6.

• C. Certo
• E. Errado