Questões sobre Outros

Com base na distribuição de freqüências do atributo X dada abaixo, assinale a opção que corresponde à estimativa da função de distribuição de X no ponto 29. Não existem observações coincidentes com os extremos das classes. Use interpolação da ogiva no cálculo da estimativa.

• A. 0,935
• B. 0,903
• C. 0,839
• D. 0,887
• E. 0,871

A figura acima caracteriza a distribuição de uma variável aleatória X, em que f(x) representa a sua função de densidade e x, os seus valores possíveis. Considerando as informações acima, julgue os itens que se seguem, referentes a probabilidade.

X tem distribuição binomial.

• C. Certo
• E. Errado

Em determinado local, há 20 pessoas que devem ser distribuídas em duas salas, A e B. Inicialmente, algumas pessoas são colocadas na sala A e o restante na sala B. Em seguida, uma pessoa entre as 20 existentes é selecionada ao acaso. Se a pessoa sorteada estiver na sala A, então ela é removida para a sala B. Caso a pessoa sorteada esteja na sala B, ela será removida para a sala A. Esse procedimento é repetido infinitamente e os sorteios entre as repetições são independentes.

Em face da situação hipotética acima e considerando que Xt seja a variável aleatória que representa o número de pessoas na sala A logo após o sorteio t, julgue os itens a seguir, acerca de processos estocásticos.

A seqüência das variáveis aleatórias X₁, X₂, ..., X_t, ... é uma cadeia de Markov.

• C. Certo
• E. Errado

Acerca das informações apresentadas acima, julgue os seguintes itens.

• C. Certo
• E. Errado

Considere a distribuição conjunta abaixo de duas variáveis aleatórias discretas X e Y. Assinale a opção que dá o valor da covariância entre X e Y.

• A.

  –6,40

• B.

  –0,87

• C.

  –0,05

• D.

  0,00

• E.

  0,25

O enunciado seguinte diz respeito às questões 54 e 55.

O vetor Y=(Y1,Y2,Y3,Y4) tem distribuição normal multivariada com vetor de médias μ=(0,1,2,0) e matriz de  ariâncias-covariâncias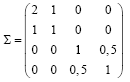

Assinale a opção correta.

• A.

  As variáveis aleatórias Y1 e Y2 são independentemente distribuídas.

• B.

  As variáveis aleatórias Y3 e Y4 são independentemente distribuídas.

• C.

  As variáveis aleatórias (Y1+Y3) e (Y2+Y4) não tem distribuição conjunta normal bivariada.

• D.

  Os vetores (Y1,Y2) e (Y3,Y4) são independentemente distribuídos.

• E.

  A variável aleatória Z=(Y1)2 + (Y2)2 tem distribuição qui-quadrado com 2 graus de liberdade.

• A.
• B.
• C.
• D.
• E. 0

Considere o processo AR(1) estacionário  com t ∈ Z(conjunto dos inteiros). A seqüência ε, é o ruído branco com variância unitária e φ = 0,5. Assinale a opção que dá o valor da função de autocovariância γ (h) do processo para h = 2.

• A.

  0,210

• B.

  0,333

• C.

  0,500

• D.

  1,000

• E.

  1,250

Uma empresa desenvolveu um sistema de coleta e transmissão de dados. Devido a reclamações por parte de um dos seus clientes, o departamento de controle de qualidade (DCQ) fez um estudo, considerando um período de 300 dias, e identificou os problemas possíveis e a freqüência esperada (em dias) de cada um deles, conforme a tabela abaixo.

Com base nessa situação hipotética, julgue os itens que se seguem.

A variável aleatória W = X + Y assume valores 0, 1 ou 2 e segue uma distribuição binomial.

• C. Certo
• E. Errado

 

Considerando as informações acima e sabendo que a eliminação da clorpropamida é predominantemente por via renal e que sua meia-vida é de aproximadamente 36 horas, julgue os itens subseqüentes.

Para se comparar os valores das glicemias do período basal a todas as outras observadas durante as 16 semanas de tratamento com a droga LAS, é correto utilizar o teste de correlação linear.

• C. Certo
• E. Errado