Questões sobre Variáveis Aleatórios

Considerando que X seja uma variável aleatória cuja função de probabilidade acumulada, F(x), é expressa por

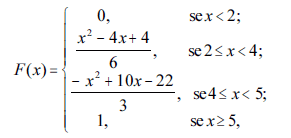
julgue os seguintes itens.

A função F(x) é contínua e diferenciável em todo o seu domínio.

• C. Certo
• E. Errado

Considerando que X seja uma variável aleatória cuja função de probabilidade acumulada, F(x), é expressa por

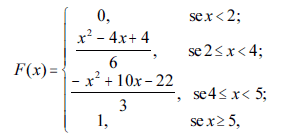
julgue os seguintes itens.

• C. Certo
• E. Errado

Com o propósito de estimar o valor do número 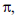, um estudante efetuará o seguinte experimento computacional:

Em relação ao experimento descrito, julgue os itens subsequentes.

O número D segue uma distribuição binomial.

• C. Certo
• E. Errado

Julgue os itens que se seguem, a respeito de análise de dados discretos.

• C. Certo
• E. Errado

Uma variável aleatória numérica contínua é uma variável que possui a característica de não se poder saber a priori o seu valor, além de ser

• A. qualitativa e de poder assumir qualquer valor dentro do intervalo no qual está definida.
• B. qualitativa e de ser fruto de um processo de contagem.
• C. qualitativa e de ser fruto de um processo de mensuração.
• D. quantitativa e de poder assumir qualquer valor dentro do intervalo no qual está definida.
• E. quantitativa e de ser fruto de um processo de contagem.

A Análise de Séries Temporais consiste no estudo de sequências numéricas, que são realizações de Processos Estocásticos. Um processo estocástico é considerado

• A. ergótico quando todas as séries temporais dele derivadas têm as mesmas estatísticas.
• B. ergótico quando suas propriedades estatísticas são invariantes no tempo.
• C. estacionário quando a série temporal dele resultante é constante.
• D. estacionário quando suas propriedades estatísticas são invariantes no tempo.
• E. estacionário quando as séries temporais dele derivadas são ergóticas.

Sejam X₁, X₂, X₃ variáveis aleatórias independentes, todas com média 100 e variância 100. O valor esperado e a variância de 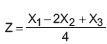 são, respectivamente,

• A.

  100 e 100

• B.

  100 e

• C.

  100 e

• D.

  0 e

• E.

  0 e

Sejam X e Y duas variáveis aleatórias independentes, correspondendo às medições realizadas por dois diferentes operadores. Essas variáveis aleatórias possuem a mesma média , mas as variâncias são diferentes, 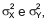 , respectivamente. Deseja-se calcular uma média ponderada dessas duas medições, ou seja, 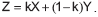. O valor de k que torna mínima a variância de Z

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Considere uma variável aleatória X com função de distribuição dada por

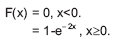
A função de densidade que representa esta variável é

• A.

  

• B.
• C.

  

• D.

  

• E.

  

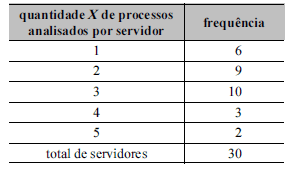
Considerando que a tabela acima mostra a distribuição de frequências da quantidade X de processos que cada servidor de certo órgão público analisou em determinada semana, julgue os itens a seguir.

A variável X é quantitativa discreta.

• C. Certo
• E. Errado