Questões de Estatística da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

Considere que o número de pousos e decolagens em um aeroporto siga um processo autorregressivo na forma , em que Z t representa o número observado de pousos e decolagens no tempo t (t = 0, 1, 2, 3, ...,NULL) e a t representa um ruído branco com média igual a zero e variância igual a 8. Com base nessas informações e considerando que , julgue os próximos itens.

A autocorrelação parcial entre Y _t e Y _t-2 é igual a zero.

• C. Certo
• E. Errado

Um estudo acerca do sucateamento de veículos automotores forneceu o modelo abaixo para a probabilidade condicional de certo tipo de veículo estar em condição de uso em função do seu tempo de uso X (em anos).

P(Y = 1|X = t) = exp(-0,4 )

Nesse modelo, exp(.) representa a função exponencial; Y é uma variável aleatória binária que assume valor 1, se o veículo estiver em condição de uso, ou 0, se o veículo não estiver em condição de uso; t 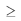 0 representa um instante (em anos) em particular; e a variável aleatória contínua X, é definida pela seguinte expressão.

P(X  t) = 1 - exp(-0,5  )

 Com base nessas informações, julgue os itens que se seguem.

A distribuição do tempo de uso do veículo pode ser corretamente representada por 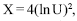, em que U é uma variável aleatória uniforme contínua no intervalo (0,1].

• C. Certo
• E. Errado

Com base nessa situação hipotética e nas informações apresentadas, julgue os próximos itens.

A correlação parcial entre X₁ e X₂ é positiva.

• C. Certo
• E. Errado

Considerando-se as informações acima, relativas a uma fila simples, baseada no processo de vida e morte, com taxas de chegada e de serviço constantes, com servidor único (s = 1), e em condição de estado de equilíbrio, julgue os itens de 89 a 93.

Em determinado instante t, o número médio de veículos no sistema de fila será igual a N_t .

• C. Certo
• E. Errado

Um porto possui dois cais para embarque ou desembarque de passageiros. Cada cais atende a uma única embarcação por vez, e assim que a operação de embarque ou desembarque é concluída, a embarcação deixa imediatamente o local para que a próxima embarcação possa ser atracada ao cais. O número de embarcações que chegam a esse porto por dia, X, segue um processo de Poisson com taxa de chegada igual a 1 embarcação/dia. Se uma embarcação chega ao porto no instante em que os dois cais estão ocupados, ela entra em uma fila única; não havendo limites para o tamanho da fila. Em cada cais, a taxa de serviço é igual a 1,5 embarcação/dia.

Considerando as informações apresentadas acima e que se trata, nessa situação, de um modelo de fila M/M/2 baseado no processo de vida e morte com taxas de chegada e de serviço constantes, julgue os itens subsequentes.

 

Considere que um acidente tenha destruído um dos cais do porto, de modo que o modelo de fila tenha passado a ser M/M/1 e que as taxas de chegada e de serviço tenham permanecido iguais a 1 embarcação/dia e 1,5 embarcação/dia, respectivamente. Nessa situação, o tamanho esperado da fila é superior a 1,5 embarcações/dia.

• C. Certo
• E. Errado

Com base nessas informações, julgue os itens a seguir.

O percentual da variação total da variável x explicada pela variável y foi inferior a 20%.

• C. Certo
• E. Errado

A mediana e a média de X são iguais.

• C. Certo
• E. Errado

 

Considerando essa situação hipotética, julgue os itens subsequentes, assumindo que exp(1) = 2,72.

O número de veículos conduzidos por pessoas portadoras de necessidades especiais que chegam ao estacionamento segue um processo de renovação.

• C. Certo
• E. Errado

A tabela a seguir apresenta a distribuição dos preços de revenda de gasolina comum, por litro, observados no levantamento realizado pela Agência Nacional do Petróleo (ANP) em outubro de 2008, na região Sudeste. A amostra consistiu de 46 valores; o menor valor observado foi R$ 2,15/litro; a média aritmética dos preços observados foi igual a R$ 2,45/litro. Essa média foi apenas 0,5% maior do que a média aritmética dos preços observados no levantamento realizado em maio de 2008.

Com base nas informações apresentadas no texto, julgue os itens que se seguem.

• C. Certo
• E. Errado

 

Considerando essa situação hipotética, julgue os itens subsequentes, assumindo que exp(1) = 2,72.

A probabilidade de a referida vaga não ser ocupada por veículo algum em determinado dia é superior a 0,15.

• C. Certo
• E. Errado