Questões de Estatística da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

Um porto possui dois cais para embarque ou desembarque de passageiros. Cada cais atende a uma única embarcação por vez, e assim que a operação de embarque ou desembarque é concluída, a embarcação deixa imediatamente o local para que a próxima embarcação possa ser atracada ao cais. O número de embarcações que chegam a esse porto por dia, X, segue um processo de Poisson com taxa de chegada igual a 1 embarcação/dia. Se uma embarcação chega ao porto no instante em que os dois cais estão ocupados, ela entra em uma fila única; não havendo limites para o tamanho da fila. Em cada cais, a taxa de serviço é igual a 1,5 embarcação/dia.

Considerando as informações apresentadas acima e que se trata, nessa situação, de um modelo de fila M/M/2 baseado no processo de vida e morte com taxas de chegada e de serviço constantes, julgue os itens subsequentes.

 

Em média, o tempo entre a chegada de uma embarcação e a da embarcação seguinte é superior a 0,9 dia.

• C. Certo
• E. Errado

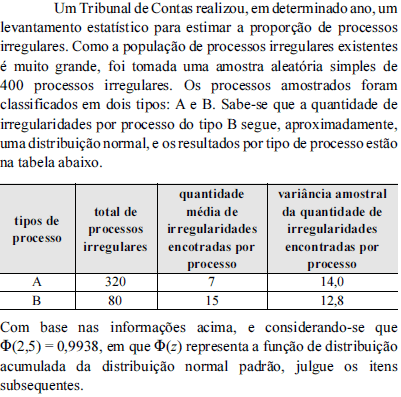
Estima-se que a mediana da quantidade de irregularidades encontradas por processo do tipo B é igual a 15.

• C. Certo
• E. Errado

 

Com base nessas informações, julgue os itens seguintes.

A função de densidade f(t) assume apenas valores entre 0 e 1.

• C. Certo
• E. Errado

Um porto possui dois cais para embarque ou desembarque de passageiros. Cada cais atende a uma única embarcação por vez, e assim que a operação de embarque ou desembarque é concluída, a embarcação deixa imediatamente o local para que a próxima embarcação possa ser atracada ao cais. O número de embarcações que chegam a esse porto por dia, X, segue um processo de Poisson com taxa de chegada igual a 1 embarcação/dia. Se uma embarcação chega ao porto no instante em que os dois cais estão ocupados, ela entra em uma fila única; não havendo limites para o tamanho da fila. Em cada cais, a taxa de serviço é igual a 1,5 embarcação/dia.

Considerando as informações apresentadas acima e que se trata, nessa situação, de um modelo de fila M/M/2 baseado no processo de vida e morte com taxas de chegada e de serviço constantes, julgue os itens subsequentes.

 

Em média, o número total de embarcações presentes no porto, atracados no cais ou na fila, é maior ou igual a 1 embarcação/dia.

• C. Certo
• E. Errado

Em um estudo oncológico, foi registrado o tempo, em semanas, de sobrevida de pacientes com leucemia aguda. Na data do diagnóstico da patologia, registrou-se também o número de glóbulos brancos, em escala logarítmica. Por meio de uma análise exploratória de dados, assumiu-se que os tempos de sobrevida ti , i = 1, ..., n, em que n é o tamanho da amostra, seguem distribuição exponencial. A tabela a seguir apresenta medidas-resumo, calculadas por meio de um software estatístico, na qual o tempo de sobrevida dos pacientes está em unidade de tempo apropriada, e o número de glóbulos brancos está em logaritmo neperiano (ln).

 

A partir dessas informações, julgue os itens a seguir.

O termo representado por é uma estatística suficiente para estimar o parâmetro da distribuição exponencial.

• C. Certo
• E. Errado

Os dados abaixo mostram os valores efetivamente gastos para o desenvolvimento de dez projetos de pesquisa (em R$ mil) selecionados ao acaso:

15 25 30 12 10 16 12 18 10 12

Com base nessas informações, julgue os itens a seguir.

Pelo coeficiente de assimetria de Pearson, a distribuição dada possui assimetria positiva.

• C. Certo
• E. Errado

Um porto possui dois cais para embarque ou desembarque de passageiros. Cada cais atende a uma única embarcação por vez, e assim que a operação de embarque ou desembarque é concluída, a embarcação deixa imediatamente o local para que a próxima embarcação possa ser atracada ao cais. O número de embarcações que chegam a esse porto por dia, X, segue um processo de Poisson com taxa de chegada igual a 1 embarcação/dia. Se uma embarcação chega ao porto no instante em que os dois cais estão ocupados, ela entra em uma fila única; não havendo limites para o tamanho da fila. Em cada cais, a taxa de serviço é igual a 1,5 embarcação/dia.

Considerando as informações apresentadas acima e que se trata, nessa situação, de um modelo de fila M/M/2 baseado no processo de vida e morte com taxas de chegada e de serviço constantes, julgue os itens subsequentes.

 

Sabendo-se que 1 dia corresponde a 24 horas, o tempo médio de espera na fila é inferior a 1 hora/embarcação.

• C. Certo
• E. Errado

O erro padrão da média amostral é inferior a 0,8 kg.

• C. Certo
• E. Errado

Um porto possui dois cais para embarque ou desembarque de passageiros. Cada cais atende a uma única embarcação por vez, e assim que a operação de embarque ou desembarque é concluída, a embarcação deixa imediatamente o local para que a próxima embarcação possa ser atracada ao cais. O número de embarcações que chegam a esse porto por dia, X, segue um processo de Poisson com taxa de chegada igual a 1 embarcação/dia. Se uma embarcação chega ao porto no instante em que os dois cais estão ocupados, ela entra em uma fila única; não havendo limites para o tamanho da fila. Em cada cais, a taxa de serviço é igual a 1,5 embarcação/dia.

Considerando as informações apresentadas acima e que se trata, nessa situação, de um modelo de fila M/M/2 baseado no processo de vida e morte com taxas de chegada e de serviço constantes, julgue os itens subsequentes.

 

Em 18 dias de funcionamento do porto, espera-se que, em média, em apenas um desses dias haja fila de embarcações.

• C. Certo
• E. Errado

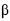Sendo os erros aleatórios distribuídos segundo uma normal, então a estimativa de máxima verossimilhança para o coeficiente  é inferior a 0,60 e superior a 0,55.

• C. Certo
• E. Errado