Questões de Estatística da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

Se a = 0,5 e b = 1,5, então a média de X é superior a 0,50.

• C. Certo
• E. Errado

Um estudo acerca do sucateamento de veículos automotores forneceu o modelo abaixo para a probabilidade condicional de certo tipo de veículo estar em condição de uso em função do seu tempo de uso X (em anos).

P(Y = 1|X = t) = exp(-0,4 )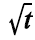

Nesse modelo, exp(.) representa a função exponencial; Y é uma variável aleatória binária que assume valor 1, se o veículo estiver em condição de uso, ou 0, se o veículo não estiver em condição de uso; t 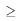 0 representa um instante (em anos) em particular; e a variável aleatória contínua X, é definida pela seguinte expressão.

P(X 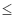 t) = 1 - exp(-0,5  )

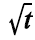 Com base nessas informações, julgue os itens que se seguem.

A probabilidade marginal P(Y = 1) é superior a 0,6.

• C. Certo
• E. Errado

A média amostral dos valores X₁, X₂, ..., X_n é o estimador de mínimos quadrados para a média da distribuição das perdas X.

• C. Certo
• E. Errado

A moda da distribuição W é igual a .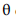

• C. Certo
• E. Errado

Um estudo acerca do sucateamento de veículos automotores forneceu o modelo abaixo para a probabilidade condicional de certo tipo de veículo estar em condição de uso em função do seu tempo de uso X (em anos).

P(Y = 1|X = t) = exp(-0,4 )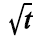

Nesse modelo, exp(.) representa a função exponencial; Y é uma variável aleatória binária que assume valor 1, se o veículo estiver em condição de uso, ou 0, se o veículo não estiver em condição de uso; t 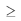 0 representa um instante (em anos) em particular; e a variável aleatória contínua X, é definida pela seguinte expressão.

P(X 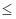 t) = 1 - exp(-0,5  )

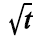 Com base nessas informações, julgue os itens que se seguem.

• C. Certo
• E. Errado

A média 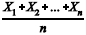 é um estimador não-tendencioso para a média da distribuição das perdas X.

• C. Certo
• E. Errado

Estima-se que a mediana e o primeiro quartil da distribuição de X na filial I são, respectivamente, iguais a 8,5 e a 7,15.

• C. Certo
• E. Errado

Considerando-se as informações acima, relativas a uma fila simples, baseada no processo de vida e morte, com taxas de chegada e de serviço constantes, com servidor único (s = 1), e em condição de estado de equilíbrio, julgue os itens de 89 a 93.

A probabilidade de que nenhum veículo esteja trafegando no trecho é igual a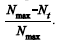

• C. Certo
• E. Errado

O número esperado de pessoas aguardando atendimento na fila é superior a 1 pessoa/minuto.

• C. Certo
• E. Errado

Considerando-se as informações acima, relativas a uma fila simples, baseada no processo de vida e morte, com taxas de chegada e de serviço constantes, com servidor único (s = 1), e em condição de estado de equilíbrio, julgue os itens de 89 a 93.

Considerando-se que o processo de chegada seja de Poisson, o intervalo médio de tempo entre chegadas de dois veículos consecutivos é igual a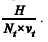

• C. Certo
• E. Errado