Questões de Estatística da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

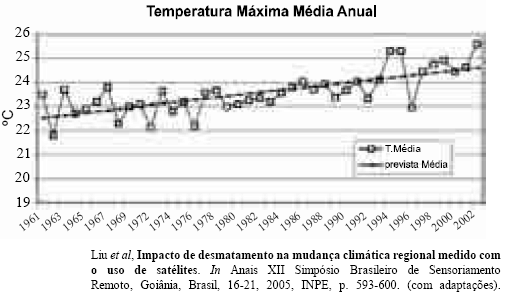
A figura acima apresenta os resultados de um estudo acerca da evolução temporal da temperatura máxima média anual — Y — de 1961 a 2002 e sua relação com o desmatamento em uma área da região amazônica. A tendência de crescimento linear foi obtida pelo método de mínimos quadrados ordinários. De acordo com esse modelo de regressão linear simples, os valores ajustados para a temperatura Y em 1961 e 2002 foram iguais a 22,5 ºC e 24,5 ºC, respectivamente, e o coeficiente de determinação (R²) foi igual a 0,72.

Com base nas informações apresentadas, julgue os itens subseqüentes.

A média histórica de Y, considerando o período de 1961 a 2002, é igual a 23,5 ºC.

• C. Certo
• E. Errado

Considere que X seja uma variável aleatória uniformemente distribuída no intervalo [0, 1]. Se X $ 0,6, então Y = 1. Se X < 0,6, então Y = 0. Um programa de computador gerou a seguinte seqüência de realizações independentes de X: 0,09 0,56 0,37 0,48 0,90. Considerando essas informações, julgue os itens subseqüentes.

Y² é uma variável aleatória de Bernoulli com probabilidade de sucesso igual a 0,8.

• C. Certo
• E. Errado

Com base nas informações apresentadas acima, e considerando que  representa a função de distribuição acumulada da distribuição normal padrão, julgue os itens de 41 a 50.

O terceiro quartil da distribuição do indicador X entre os agricultores aderentes ao PRONAF observados na amostra é superior a 0,80.

• C. Certo
• E. Errado

Uma prefeitura registrou o aumento do valor venal V (em R$ por metro quadrado) de 200 imóveis localizados em certo bairro residencial, conforme apresentado na tabela a seguir.

Com base nessas informações, julgue os itens a seguir.

O aumento médio por imóvel registrado pela prefeitura foi inferior a R$ 12,50/m² e superior a R$ 5,50/m².

• C. Certo
• E. Errado

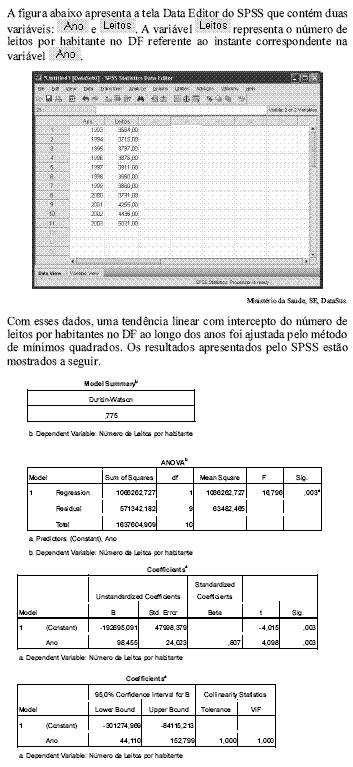
Tendo como referência essas informações, julgue os itens de 64 a 76.

O intervalo de confiança de 95% para o coeficiente angular da reta de regressão, sob a hipótese de normalidade dos erros aleatórios, é obtido com base em uma distribuição t de Student com 2 graus de liberdade.

• C. Certo
• E. Errado

Considere que X seja uma variável aleatória uniformemente distribuída no intervalo [0, 1]. Se X $ 0,6, então Y = 1. Se X < 0,6, então Y = 0. Um programa de computador gerou a seguinte seqüência de realizações independentes de X: 0,09 0,56 0,37 0,48 0,90. Considerando essas informações, julgue os itens subseqüentes.

X² é uma variável aleatória uniformemente distribuída no intervalo [0, 1].

• C. Certo
• E. Errado

Com base nessas informações e considerando que o valor 100 é representado nesses diagramas como 10|0, julgue os itens que se seguem.

Considerando que a correlação entre X e Y seja igual a 0,95, então a variação da distribuição dos tempos X explica pelo menos 94% da variação da distribuição da variável Y.

• C. Certo
• E. Errado

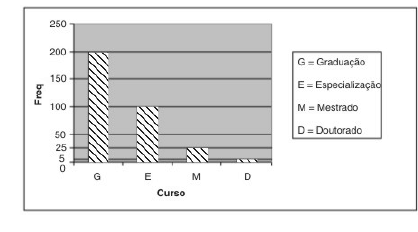
A qualificação dos professores é de grande importância para a qualidade da formação dos estudantes. Considerando que a figura acima apresenta a distribuição do número de professores em uma faculdade, segundo a formação acadêmica (curso), julgue os itens de 77 a 85.

Caso a distribuição mostrada na figura fosse apresentada em um gráfico de setores, o ângulo do setor correspondente à categoria especialização seria superior a 100º.

• C. Certo
• E. Errado

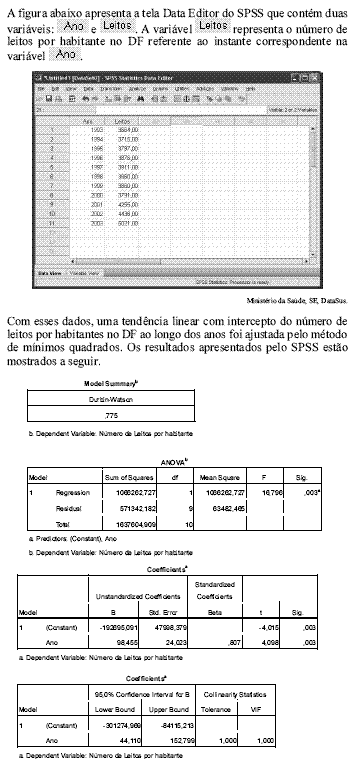
Tendo como referência essas informações, julgue os itens de 64 a 76.

A estimativa do desvio padrão residual é inferior a 300.

• C. Certo
• E. Errado

A variância de R é igual a F2 .

• C. Certo
• E. Errado