Questões de Estatística da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

Considerando que X1, X2,..., X10 representa uma amostra aleatória simples desse indicador, julgue os próximos itens.

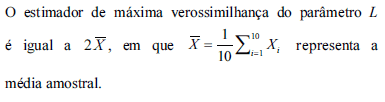
• C. Certo
• E. Errado

Alunos de um departamento de uma universidade estudaram por dois livros diferentes, A e P. Foram retiradas amostras aleatórias simples dos que estudaram pelo livro A e dos que estudaram pelo livro P, tendo sido observadas as notas dos alunos em um exame padronizado. Um teste t de Student foi aplicado com a hipótese nula H₀: μ_A = μ_P e a hipótese alternativa H₁: μ_A > μ_P, em que μA e μP representam, respectivamente, as médias populacionais das notas dos alunos, no exame padronizado, que estudaram pelo livro A e pelo livro P. O valor p obtido foi 0,03.

A partir da situação apresentada, julgue os itens subsequentes, considerando o nível de significância de 0,05.

As hipóteses do teste t de Student aplicado são simples.

• C. Certo
• E. Errado

A estimativa da variância V é igual ou inferior a 1,5.

• C. Certo
• E. Errado

Alunos de um departamento de uma universidade estudaram por dois livros diferentes, A e P. Foram retiradas amostras aleatórias simples dos que estudaram pelo livro A e dos que estudaram pelo livro P, tendo sido observadas as notas dos alunos em um exame padronizado. Um teste t de Student foi aplicado com a hipótese nula H₀: μ_A = μ_P e a hipótese alternativa H₁: μ_A > μ_P, em que μA e μP representam, respectivamente, as médias populacionais das notas dos alunos, no exame padronizado, que estudaram pelo livro A e pelo livro P. O valor p obtido foi 0,03.

A partir da situação apresentada, julgue os itens subsequentes, considerando o nível de significância de 0,05.

• C. Certo
• E. Errado

A variável aleatória y_k, para k = 1, þ, 5, segue uma distribuição normal com variância V.

• C. Certo
• E. Errado

Alunos de um departamento de uma universidade estudaram por dois livros diferentes, A e P. Foram retiradas amostras aleatórias simples dos que estudaram pelo livro A e dos que estudaram pelo livro P, tendo sido observadas as notas dos alunos em um exame padronizado. Um teste t de Student foi aplicado com a hipótese nula H₀: μ_A = μ_P e a hipótese alternativa H₁: μ_A > μ_P, em que μA e μP representam, respectivamente, as médias populacionais das notas dos alunos, no exame padronizado, que estudaram pelo livro A e pelo livro P. O valor p obtido foi 0,03.

A partir da situação apresentada, julgue os itens subsequentes, considerando o nível de significância de 0,05.

• C. Certo
• E. Errado

A estimativa de mínimos quadrados ordinários do coeficiente a é igual ou superior a 1.

• C. Certo
• E. Errado

Alunos de um departamento de uma universidade estudaram por dois livros diferentes, A e P. Foram retiradas amostras aleatórias simples dos que estudaram pelo livro A e dos que estudaram pelo livro P, tendo sido observadas as notas dos alunos em um exame padronizado. Um teste t de Student foi aplicado com a hipótese nula H₀: μ_A = μ_P e a hipótese alternativa H₁: μ_A > μ_P, em que μA e μP representam, respectivamente, as médias populacionais das notas dos alunos, no exame padronizado, que estudaram pelo livro A e pelo livro P. O valor p obtido foi 0,03.

A partir da situação apresentada, julgue os itens subsequentes, considerando o nível de significância de 0,05.

Caso fosse calculado um intervalo de confiança bilateral para μ_A – μ_P, com coeficiente de confiança 95%, tal intervalo conteria o valor zero.

• C. Certo
• E. Errado

Os limites inferiores e superiores do intervalo de confiança de máxima verossimilhança para ln(λ) podem ser obtidos calculando-se a função logarítmica (ln), respectivamente, nos limites inferiores e superiores do intervalo de confiança de máxima verossimilhança para λ.

• C. Certo
• E. Errado

O estimador de ln(λ) via máxima verossimilhança é In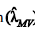

• C. Certo
• E. Errado