Questões de Matemática do ano 2002

Considere que, durante uma certa epidemia, cada indivíduo, começando no dia seguinte ao que foi infectado pelo vírus transmissor da doença e durante 10 dias consecutivos, contamine diariamente um outro indivíduo. Assim, se um indivíduo é infectado no dia 0, no dia 1, ele continuará infectado e contaminará mais um indivíduo; no dia 2, serão 4 indivíduos infectados, e assim por diante. No dia 11, o ciclo de vida do vírus completa-se para o primeiro indivíduo infectado, que, então, livra-se da doença, o mesmo se repetindo para os demais indivíduos, quando se completam 11 dias após eles serem infectados. Com base nessa situação hipotética, representando por a_n o número de indivíduos infectados n dias após a ocorrência da primeira infecção por esse vírus e supondo a₀ = 1, julgue os itens a seguir.

• C. Certo
• E. Errado

Acerca de aspectos estruturais e das idéias do texto acima, julgue os seguintes itens.

Se o percentual de crescimento do número de correntistas pessoa física do BB, verificado em 2001, se mantiver para 2002 e 2003, então, ao final de 2003, o BB terá mais de 16 milhões de correntistas.

• C. Certo
• E. Errado

Observe a seqüência de números a seguir:

2,5       6,5       14,5     30,5 ...

O segundo número (6,5) foi obtido aplicando uma equação de 1o grau ao primeiro (2,5), ou seja, se x1 e x2 representam, respectivamente, os dois primeiro números,

 x₂ = ax₁ + b

do mesmo modo, o terceiro número x3 foi obtido aplicando a mesma equação ao segundo, ou seja,

x₃ = ax₂ + b

e assim sucessivamente. O quinto número desta seqüência será então igual a:

• A.

  46,5;

• B.

  52,5;

• C.

  56,5;

• D.

  62,5;

• E.

  66,5.

55 - Dois amigos decidiram só trocar correspondências na internet por intermédio de códigos. Eles combinaram, a partir de um determinado dia, usar as 26 letras

ABCDEFGHIJKLMNOPQRSTUVWXYZ

do seguinte modo: no primeiro dia, cada letra vira a seguinte neste alfabeto, ou seja, A vira B, B vira C e assim por diante, até Z, que vira A.

Por exemplo, a palavra HOJE seria escrita como IPKF. No segundo dia, pula mais uma letra, ou seja, A vira C, B vira D e assim por diante. Note que, neste segundo dia, Y vira A e Z vira B. No terceiro dia pula mais uma letra, ou seja, A vira D, B vira E etc. e assim sucessivamente ao longo dos dias. É claro que no vigésimo-sexto dia A viraria A, o código seria desfeito e a mensagem poderia ser lida por quem não conhece o código. Para evitar isto, no vigésimo-sexto dia os amigos voltam a usar o código do primeiro dia e assim por diante.

Neste caso, se um amigo, no 569o dia, quiser dizer AMIGO deverá escrever:

• A.

  ZLHFN;

• B.

  DPLJR;

• C.

  EQMKS;

• D.

  FRNLT;

• E.

  YKGEM.

Um cartaz digital de propaganda apresenta a logomarca do anunciante, que tem forma circular, da seguinte maneira: num determinado momento, a marca está na posição 1; passado 1min a marca aparece na posição 2, no minuto seguinte ela vai para a posição 3, no minuto seguinte para a posição 4, um minuto depois para a posição 5 e, no 5o minuto, volta para a posição 1, reiniciando o ciclo como mostra a figura:

Uma pessoa começa a observar o cartaz num instante em que a marca está na posição 1. Passadas 2h1min, a marca estará na seguinte posição:

• A.

  1;

• B.

  2;

• C.

  3:

• D.

  4;

• E.

  5.

Considere o seguinte enunciado para responder às questões de números 23 e 24.

Em uma livraria foi montado um serviço de utilização de microcomputadores. O usuário paga uma taxa fixa de R$ 1,50, acrescida de R$ 2,50 por hora. Fração de hora é cobrada como hora inteira.

A quantia a ser desembolsada por uma pessoa que utilize certo dia esse serviço, das 12h50min às 16h15min, é

• A.

  R$ 11,50

• B.

  R$ 11,00

• C.

  R$ 10,00

• D.

  R$ 9,50

• E.

  R$ 9,00

Um prédio de 8 andares tem, em cada andar, 4 janelas de vidro, retangulares, medindo 2,5m por 1,0m. A área total dos vidros utilizados nessas janelas, em m², é de:

• A.

  90

• B.

  85

• C.

  80

• D.

  75

Em um triângulo retângulo, um dos ângulos agudos mede 17/30 do outro. A soma dos dois ângulos agudos desse triângulo é:

• A.

  75^o

• B.

  80^o

• C.

  85^o

• D.

  90^o

Uma parede retangular de 4,40m por 2,50m tem duas portas de 1,80m por 1m. A área da superfície da parede é de:

• A.

  6,0m²

• B.

  7,4m²

• C.

  8,0m²

• D.

  9,4m²

Uma pessoa tem dois terrenos. O terreno I tem forma de um quadrado de lado igual a 20 m. Nesse quadrado, ela inscreve uma circunferência, usando a parte externa à circunferência para lazer. O terreno II tem a forma de um retângulo com um dos lados medindo 16 m. Neste terreno, ela separa uma faixa retangular de terra por uma reta paralela ao lado de 16 m, usando o retângulo menor para lazer: este retângulo tem 80 m2 de área, que representa 20% da área total do terreno II.

Com base nessas informações, julgue os itens seguintes, considerando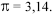

O comprimento da circunferência inscrita no terreno I é menor que 60 m.

• C. Certo
• E. Errado