Questões de Matemática do ano 2007

Um torneio de futebol foi disputado por apenas 4 equipes.Cada uma delas jogou uma única vez com todas as outras.Na tabela, cada célula representa o no de gols que o time da linha marcou no time da coluna. Por exemplo, a equipe W marcou 3 gols sobre a equipe Y.

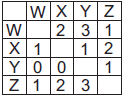
Nesse torneio, cada vitória vale 3 pontos. Empate vale 1 e derrota não dá ponto algum. Com relação à colocação final dos times no torneio, conclui-se corretamente que:

• A. W foi o segundo.
• B. X foi o segundo.
• C. X foi o terceiro.
• D. Z foi o terceiro.
• E. Z foi o último.

Num mesmo dia, uma mercadoria foi comprada por R$ 70,00, vendida por R$ 80,00, recomprada por R$ 90,00 e, finalmente, vendida por R$ 100,00. No final dessa seqüência de compras e vendas, o dono dessa mercadoria:

• A. teve um lucro de R$ 10,00.
• B. teve um prejuízo de R$ 10,00.
• C. teve um prejuízo de R$ 20,00.
• D. teve um lucro de R$ 20,00.
• E. não teve lucro nem prejuízo.

Para enfeitar toalhas retangulares de 2,0 m de comprimento por 1,60 m de largura, uma costureira colocará fita colorida ao redor de toda a borda de cada uma delas. Assim, com 30 m de fita, o número de toalhas que poderão ser enfeitadas é:

• A. 6.
• B. 5.
• C. 4.
• D. 3.
• E. 2.

A cantina de uma escola serve, na merenda, leite com groselha, sendo que para cada 300 mL de leite são adicionados 50 mL de groselha. Se em determinado dia forem servidos 56 litros dessa mistura (leite + groselha), a quantidade de litros de groselha a serem utilizados será

• A. 9.
• B. 8.
• C. 7.
• D. 6.
• E. 5.

Um painel decorativo de madeira foi pintado conforme indicam as partes hachuradas na figura, onde todas as medidas estão em cm.

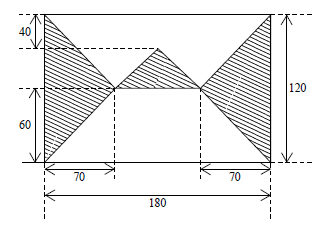
• A. 11/4.
• B. 11/6.
• C. 11/8.
• D. 11/16.
• E. 11/32.

Um nanômetro é, por definição, um bilionésimo de um metro. Antônio Maria tem 1,64m de altura. A altura de Antônio Maria em nanômetros é igual a:

• A. 0,000000164;
• B. 1,64;
• C. 16.400.000;
• D. 164.000.000;
• E. 1.640.000.000.

Avalie se os quatro números a seguir são divisíveis por

3: 300 ; 333.333.333 ; 3.444.444.444.444.444 ;

11.111.111.111.111.111.111.111.111.111

A quantidade de números divisíveis por 3 é:

• A. 0;
• B. 1;
• C. 2;
• D. 3;
• E. 4;

O resultado d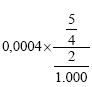e  é:

• A. 0,25;
• B. 1;
• C. 40;
• D. 200;
• E. 5.000.

Para analisar as afirmações seguintes, considere que x é um número par e y é um número ímpar.

I. 3x+ 2y é um número ímpar.

II. 5xy é um número par.

III. x² − y² é um número ímpar.

É correto afirmar que

• A. I, II e III são verdadeiras.
• B. somente uma das afirmações é verdadeira.
• C. somente I e II são verdadeiras.
• D. somente I e III são verdadeiras.
• E. somente II e III são verdadeiras.

• A. negativo.
• B. compreendido entre 0 e 1.
• C. compreendido entre 1 e 2.
• D. compreendido entre 2 e 3.
• E. maior do que 3.