Questões de Matemática do ano 2020
Lista completa de Questões de Matemática do ano 2020 para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Em uma cesta existem x maçãs verdes e y maçãs vermelhas com x e y sendo números inteiros positivos. Após adicionar 15 maças verdes à cesta, o percentual da quantidade de maças verdes passou a ser 60% da quantidade total de maçãs. A opção que contém a relação correta entre x e y é:
-
A) x + 15 = 3y
B) 2x+15 = 3y
C) 2x + 30 = 3y
D) 2x + 30 = 4y
E) 2x + 40 = 3y
Um estudante piauiense criou uma calculadora com uma propriedade diferente das calculadoras habituais. Se no visor estiver o número n, ao apertar a tecla #, a calculadora exibe na tela o número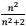 
. Se no visor estiver o número 2, ao apertar a tecla # três vezes consecutivas, o número que aparecerá na tela será:
-
A) 2/123
B) 3/123
C) 4/123
D) 5/123
E) 6/123
Um empresário piauiense produz x unidades de garrafas de cajuína a cada 3 dias e y potes de doce de caju a cada 4 dias. Se um lote de cajuína para venda contém 5 unidades de cajuína e um lote de doce de caju possui 6 unidades de potes de caju, após 120 dias o produto entre a quantidade de lotes de cajuína e a quantidade de lotes de doce de caju disponíveis para venda é:
-
A) 15xy
B) 20xy
C) 30xy
D) 40xy
E) 60xy
Resolvendo-se a inequação log 2x > log (x + 1), obtemos:
-
A) S = {x ? R I x < -1}
B) S = {x ? R I x > -1}
C) S = {x ? R I x >1}
D) S = {x ? R I x > 1/2}
E) S = {x ? R I x < 1/2}
Os coeficientes angular e linear da reta r, que passa por A (0, 2) e B (1, 3), são, respectivamente:
-
A) 1 e 2.
B) -1 e 0.
C) 1 e -2.
D) 2 e 0.
E) - 1 e 2.
Em um único sorteio envolvendo os números naturais de 1 a 200, a probabilidade de sair um número que não seja múltiplo de sete é:
-
A) 82%.
B) 81%.
C) 85%.
D) 86%.
E) 80%.
Escreva a equação geral da circunferência, que tem centro C (-2, 1) e raio r = ?5.
-
A) x² + y² + 4x - 2y =0.
B) x² + y² - 4x + 2y - 1 =0.
C) x² - y² + 5x - y =0.
D) x² - y² - 4x + y -2 =0.
E) 2x² - y² + 4x - y -5 =0.
Um prisma de base quadrangular possui volume igual a 108 cm³. Determine sua altura sabendo que ela corresponde ao triplo da medida da aresta da base.
-
A) 5 cm.
B) 10 cm.
C) 15 cm.
D) 25 cm.
E) 30 cm.
Sendo f(x) = ax , a > 0 e a ? 1, onde m e n números reais quaisquer, analise e classifique os itens.
I - f( m + n) = f(m) + f(n) II - f( m + n) = f(m) . f(n) III - f(m . n) = f(m) . f(n) IV - f(m . n) =(f(m))n V - f (m - n) = f(m) : f(n)
Assinale a alternativa que contém as afirmativas CORRETAS:
I - f( m + n) = f(m) + f(n) II - f( m + n) = f(m) . f(n) III - f(m . n) = f(m) . f(n) IV - f(m . n) =(f(m))n V - f (m - n) = f(m) : f(n)
Assinale a alternativa que contém as afirmativas CORRETAS:
-
A) II, III e IV, apenas.
B) II, IV e V, apenas.
C) III, IV e V, apenas.
D) I, II e IV, apenas.
E) I, III e IV, apenas.
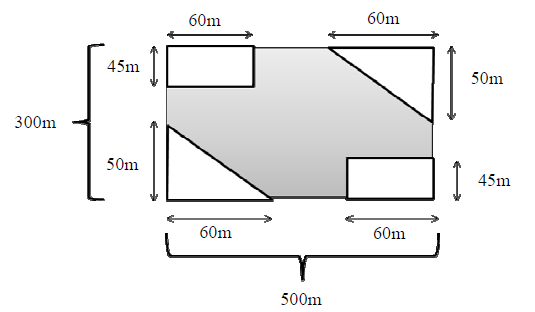
Uma praça está inscrita em uma área retangular cujos lados medem 300 m e 500 m, conforme a figura abaixo. Calculando a área da praça, quanto obtemos? Note que a praça é referente à área sombreada.
-
A) 138.600 cm²
B) 141.600 cm²
C) 147.000 cm².
D) 128.300 cm²
E) 148.600 cm².
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
