Questões sobre Equações Exponenciais

Julgue os itens subseqüentes.

A solução da equação 15 × 2^x = 960 é superior a 5.

• C. Certo
• E. Errado

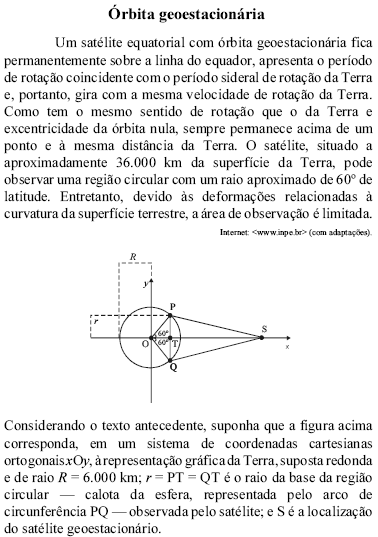
Com base no texto e nessas informações, julgue os itens seguintes.

• C. Certo
• E. Errado

O valor da expressão aritmética: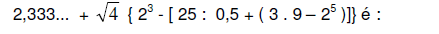

• A. um número natural.
• B. um número inteiro negativo.
• C. um número racional.
• D. um número irracional.

Em 2006, a diretoria de uma fábrica de autopeças estabeleceu como meta aumentar em 5%, a cada ano, os lucros obtidos com as vendas de seus produtos. Considere que, em 2006, o lucro tenha sido de x reais. Se a meta for cumprida, o lucro dessa empresa, em 2010, será de

• A.

  (0,05)⁴. x

• B.

  (1,05)⁴. x

• C.

  (1,50)⁴ . x

• D.

  (1,20) . x

• E.

  (4,20) . x

Considerando as funções f (x) = ln x e g(x) = e ^x , assinale a opção correta.

• A.

  A derivada de primeira ordem da função f (x) é sempre negativa.

• B.

  A derivada de segunda ordem de g(x) é sempre negativa.

• C.

  As funções f (x) e g(x) têm mesmo domínio.

• D.

  Existe algum número real x tal que f (x) = g(x).

• E.

  f (x) e g(x) são inversíveis e f (g(x)) = g(f (x)) = x, para todo x > 0.

Se x é um número real e exp(x² - 5x + 6) = 1, então

• A.

  x = 2 ou x =3.

• B.

  x = 1 ou x= 2.

• C.

  x = 0 ou x = 3.

• D.

  x = -1 ou x = 0.

• E.

  x = -1 ou x= 4.

Julgue os itens subseqüentes.

A solução da equação 15 × 2 ^x = 960 é superior a 5.

• C. Certo
• E. Errado

Utilizando um programa computacional gráfico, um aluno do ensino médio desenhou, para alguns valores constantes k > 0, o gráfico da função exponencial y = k ax, em que a é uma constante. Esses gráficos estão ilustrados na figura abaixo.

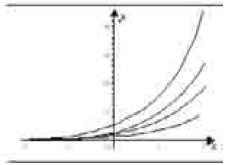
Com base nessas informações e na figura acima, julgue os itens a seguir.

Considere que o aluno tenha desenhado também o gráfico da função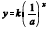   no mesmo sistema de coordenadas. Nesse caso, esse gráfico seria simétrico ao gráfico de y = k ax em relação à reta y = x.

• C. Certo
• E. Errado

Utilizando um programa computacional gráfico, um aluno do ensino médio desenhou, para alguns valores constantes k > 0, o gráfico da função exponencial y = k ax, em que a é uma constante. Esses gráficos estão ilustrados na figura abaixo.

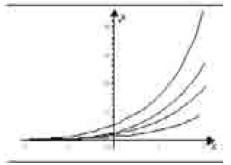
Com base nessas informações e na figura acima, julgue os itens a seguir.

Para uma mesma abscissa x, considere os pontos de coordenadas (x, k ax ) para os diferentes valores de k. Nessa situação, o ponto que está mais próximo do eixo Ox é aquele que está sobre o gráfico da função em que o coeficiente k é o maior possível.

• C. Certo
• E. Errado

Utilizando um programa computacional gráfico, um aluno do ensino médio desenhou, para alguns valores constantes k > 0, o gráfico da função exponencial y = k ax, em que a é uma constante. Esses gráficos estão ilustrados na figura abaixo.

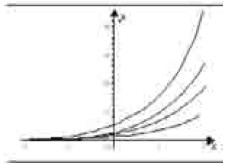
Com base nessas informações e na figura acima, julgue os itens a seguir.

Infere-se dos gráficos que 0 < a < 1.

• C. Certo
• E. Errado