Questões sobre Equações Exponenciais

Utilizando um programa computacional gráfico, um aluno do ensino médio desenhou, para alguns valores constantes k > 0, o gráfico da função exponencial y = k ax, em que a é uma constante. Esses gráficos estão ilustrados na figura abaixo.

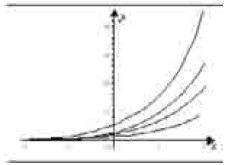
Com base nessas informações e na figura acima, julgue os itens a seguir.

Para cada valor de k o gráfico correspondente à função y = k ax intercepta o eixo Oy no ponto de coordenadas (0, k).

• C. Certo
• E. Errado

Julgue os itens subseqüentes.

A solução da equação 15 × 2 ^x = 960 é superior a 5.

• C. Certo
• E. Errado

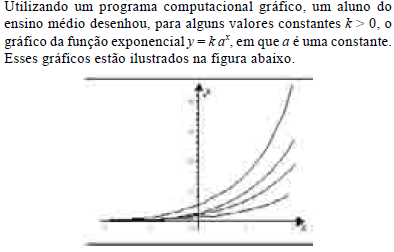
Com base nessas informações e na figura acima, julgue os itens a seguir.

Infere-se dos gráficos que 0 < a < 1.

• C. Certo
• E. Errado

• A.

• B.
• C.

• D.

• E.

Ao discutir a ampliação do estudo da potenciação envolvendo expoentes naturais para o estudo da potenciação com expoente inteiro negativo, os PCN − Matemática sugerem um contexto que envolva

• A.

  as idéias veiculadas pelas operações de adição e subtração de números inteiros.

• B.

  a grandeza tempo e suas unidades de medida, por manterem uma relação não decimal.

• C.

  a exploração dos aspectos numéricos que caracterizam os poliedros convexos.

• D.

  o registro, a comparação e/ou cálculo com números muito grandes ou muito pequenos.

• E.

  a elaboração de tabelas e gráficos, a partir da coleta e organização de dados.

Uma certa substância se desintegra seguindo a lei: M(t) = k.3 −^0,5t, onde M (t) é a massa da substância (gramas) presente no instante t (minutos) e k é uma constante. O tempo necessário para que esta substância se reduza a 1/3 da quantidade inicial (no instante t =0) é:

• A. 2min;
• B. 3min;
• C. 4min;
• D. 5min;
• E. 6min;

O número total de hambúrgueres vendidos por uma cadeia de lanchonetes está aumentando exponencialmente. Se 4 bilhões de sanduíches foram vendidos em 1995 e 12 bilhões foram vendidos no ano 2000, quantos serão vendidos em 2005?

• A. 20 bilhões
• B. 26 bilhões
• C. 42 bilhões
• D. 30 bilhões
• E. 36 bilhões

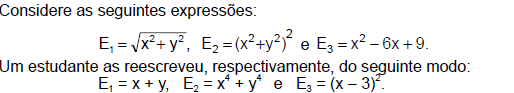
Em relação a essa reescrita, é correto afirmar:

• A. E₁ foi reescrita corretamente.
• B. Apenas E₃ foi reescrita corretamente.
• C. E₁ e E₃ foram devidamente reescritas.
• D. Apenas E₂ foi reescrita do modo correto.
• E. Todas foram reescritas corretamente.

A dosagem mínima para certo medicamento ter eficácia é de 8 mg no organismo de uma pessoa com certa doença. Sabe-se que t horas depois de ministrados M_o mg deste medicamento, a quantidade residual em mg do mesmo é dada pela lei rt M =M_o . 2-^rt . Para um certo paciente, foram ministrados 128 mg deste medicamento às 8 horas da manhã e, 4 horas depois, verificou-se que a quantidade residual era 16 mg. Para que o medicamento mantenha sua eficácia, a nova dose deve ser ministrada no seguinte horário:

• A. 11 h 20 min
• B. 12 h 20 min
• C. 13 h 20 min
• D. 14 h 20 min

Se 2^x +2^-x =m, então 4^x +4^-x é igual a

• A.

  m² – 4

• B.

  m²– 2

• C.

  m²+ 2

• D.

  m²+ 4