Questões sobre Funções
Lista completa de Questões sobre Funções para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Sendo uma função, definida no conjunto dos números reais positivos, tal que (x + 1) = x(x) e (1) = 1, julgue o item.
(0) = 0
(0) = 0
Determine o ponto no qual a função quadrática: Y = 2x² 5x + 3 corta o eixo da ordenada:
-
A) (0 , 3)
B) (3 , 0)
C) (0 , 6)
D) (0 , 0)
Qual o valor de x na balança representada abaixo?
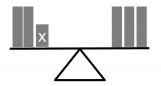

-
A) X = 1.
B) X = 3,5.
C) X = 1,5.
D) X = 2.
E) X = 6.
Considere as funções quadráticas f(x) = a1x2 + b1x + c1 e g(x) = a2x2 + b2x + c2, em que a1, b1, c1, a2, b2 e c2 são constantes, a1 > 0 e a2 < 0. Acerca dessas funções, julgue os itens seguintes, considerando o plano cartesiano usual xOy.
I O gráfico da função f é uma parábola com concavidade voltada para cima; o gráfico da função g é uma parábola com concavidade voltada para baixo. II Os gráficos das funções f e g podem: não possuir pontos em comum; possuir um único ponto em comum; possuir dois pontos distintos em comum.
III Já que a1 > 0, o gráfico da função f pode não interceptar o eixo Ox, mas necessariamente intercepta o eixo Oy. Por outro lado, já que a2 < 0, o gráfico da função g pode não interceptar o eixo Oy, mas necessariamente intercepta o eixo Ox.
Assinale a opção correta.
I O gráfico da função f é uma parábola com concavidade voltada para cima; o gráfico da função g é uma parábola com concavidade voltada para baixo. II Os gráficos das funções f e g podem: não possuir pontos em comum; possuir um único ponto em comum; possuir dois pontos distintos em comum.
III Já que a1 > 0, o gráfico da função f pode não interceptar o eixo Ox, mas necessariamente intercepta o eixo Oy. Por outro lado, já que a2 < 0, o gráfico da função g pode não interceptar o eixo Oy, mas necessariamente intercepta o eixo Ox.
Assinale a opção correta.
-
A) Apenas o item I está certo.
B) Apenas os itens I e II estão certos.
C) Apenas os itens I e III estão certos.
D) Apenas os itens II e III estão certos.
E) Todos os itens estão certos.
Ao receber uma demanda por equipamentos para coleta de dados, a fábrica Alfa verificou que possuía 40.000 unidades desse equipamento em estoque e que era capaz de produzir 10.000 novas unidades por mês. Assim, a quantidade q desses equipamentos que essa fábrica pode fornecer, em milhares de unidades, decorridos x meses desde a data de recebimento da demanda, pode ser modelada pela função q(x) = 10x + 40. Por outro lado, a necessidade n desses equipamentos, em milhares de unidades, decorridos x meses desde o início das capacitações das equipes de campo, pode ser modelada pela função n(x) = 5x2 .
Com base nessas informações, considerando-se que o início das capacitações das equipes de campo e o recebimento da demanda pela fábrica Alfa ocorreram no mesmo dia D, conclui-se, de acordo com os modelos propostos, que a necessidade por esses equipamentos irá igualar a quantidade desses equipamentos que pode ser fornecida pela fábrica Alfa quando decorridos
Com base nessas informações, considerando-se que o início das capacitações das equipes de campo e o recebimento da demanda pela fábrica Alfa ocorreram no mesmo dia D, conclui-se, de acordo com os modelos propostos, que a necessidade por esses equipamentos irá igualar a quantidade desses equipamentos que pode ser fornecida pela fábrica Alfa quando decorridos
-
A) 2 meses desde o dia D.
B) 3 meses desde o dia D.
C) 4 meses desde o dia D.
D) 5 meses desde o dia D.
E) 6 meses desde o dia D.
Sabendo que 2 é uma das raízes de x2 + p . x - 6 = 0 , assinale a alternativa que apresenta a outra raiz da equação.
-
A) -3
B) -1
C) 1
D) 3

Se x = 3 é uma das raízes da equação ax 2 - 4 = 0, então o valor de a é:
-
A) 1/3.
B) 2/3.
C) 4/9.
D) 5/9.
E) 7/9.

O valor de x que resolve a proporção 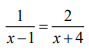 é :
é :
-
A) x = 5.
B) x = 6.
C) x = 7.
D) x = 8.
E) x = 9.
Considere a função real f(x) = |x ? 4| que também pode ser representada pelo gráfico abaixo e assinale a alternativa CORRETA.
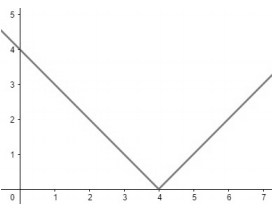

-
A) f(?1) = ?5.
B) f(?3) + f(3) = 0.
C) f(?2) = f(10).
D) f(4) = f(?4).
E) f(0) = ?4.
Considerando as seguintes frações: f(x) = 2x + 8 e g(x) = 3x 2, assinale a alternativa que apresenta o resultado de f(6)/g(2).
-
A) 3.
B) 5.
C) 8.
D) 16.
E) 24.


