Questões de Raciocínio lógico
Lista completa de Questões de Raciocínio lógico para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Raciocínio lógico - Proposição/Argumento - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2008

A partir das informações e do diálogo acima, julgue os itens que se seguem.
A sentença (5) é F.- C. Certo
- E. Errado
Trinta lojistas compraram, para revender, calças, camisas e vestidos, em uma fábrica de confecções. Sabe-se que dos 30 lojistas: I apenas 3 compraram os três produtos referidos; II 9 compraram calças e vestidos; III 6 compraram camisas e vestidos; IV 3 compraram apenas camisas; V 9 compraram camisas; VI 15 compraram vestidos. O número de lojistas que compraram apenas vestidos é igual a
- A. 2
- B. 3
- C. 4
- D. 5
Raciocínio lógico - Proposição/Argumento - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2008

A partir das informações e do diálogo acima, julgue os itens que se seguem.
A frase indicada por (3) não é uma proposição.- C. Certo
- E. Errado
Raciocínio lógico - Proposição/Argumento - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2008
Uma proposição é uma oração declarativa — não é exclamativa nem interrogativa — que pode ser julgada como verdadeira (V) ou falsa (F). As proposições são representadas por letras p, q, r, s etc. Dada uma proposição p, a negação de p, indicada por ¬p, tem sempre o valor oposto ao de p. A partir de proposições dadas, pode-se construir novas proposições mediante o emprego de conectivos: o conectivo 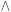 colocado entre as proposições p e q dá origem à proposição p
colocado entre as proposições p e q dá origem à proposição p q (lê-se: p e q), que é V somente se ambas as proposições forem V, caso contrário, será F; o conectivo
q (lê-se: p e q), que é V somente se ambas as proposições forem V, caso contrário, será F; o conectivo 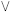 colocado entre as proposições p e q origina a proposição p
colocado entre as proposições p e q origina a proposição p q (lê-se: p ou q), que é F somente se ambas as proposições forem F, caso contrário, será V; e o conectivo → colocado entre as proposições p e q forma a proposição p → q (lê-se: se p então q), que é F somente se p for V e q for F, caso contrário, será sempre V. Uma proposição r formada a partir de outras proposições é uma tautologia se r tiver sempre o valor lógico V independentemente dos valores lógicos das proposições que a formam. A partir dessas informações, julgue os itens que se seguem.
q (lê-se: p ou q), que é F somente se ambas as proposições forem F, caso contrário, será V; e o conectivo → colocado entre as proposições p e q forma a proposição p → q (lê-se: se p então q), que é F somente se p for V e q for F, caso contrário, será sempre V. Uma proposição r formada a partir de outras proposições é uma tautologia se r tiver sempre o valor lógico V independentemente dos valores lógicos das proposições que a formam. A partir dessas informações, julgue os itens que se seguem.
- C. Certo
- E. Errado
Raciocínio lógico - Proposição/Argumento - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2008
Uma proposição é uma oração declarativa — não é exclamativa nem interrogativa — que pode ser julgada como verdadeira (V) ou falsa (F). As proposições são representadas por letras p, q, r, s etc. Dada uma proposição p, a negação de p, indicada por ¬p, tem sempre o valor oposto ao de p. A partir de proposições dadas, pode-se construir novas proposições mediante o emprego de conectivos: o conectivo  colocado entre as proposições p e q dá origem à proposição p
colocado entre as proposições p e q dá origem à proposição p q (lê-se: p e q), que é V somente se ambas as proposições forem V, caso contrário, será F; o conectivo
q (lê-se: p e q), que é V somente se ambas as proposições forem V, caso contrário, será F; o conectivo  colocado entre as proposições p e q origina a proposição p
colocado entre as proposições p e q origina a proposição p q (lê-se: p ou q), que é F somente se ambas as proposições forem F, caso contrário, será V; e o conectivo → colocado entre as proposições p e q forma a proposição p → q (lê-se: se p então q), que é F somente se p for V e q for F, caso contrário, será sempre V. Uma proposição r formada a partir de outras proposições é uma tautologia se r tiver sempre o valor lógico V independentemente dos valores lógicos das proposições que a formam. A partir dessas informações, julgue os itens que se seguem.
q (lê-se: p ou q), que é F somente se ambas as proposições forem F, caso contrário, será V; e o conectivo → colocado entre as proposições p e q forma a proposição p → q (lê-se: se p então q), que é F somente se p for V e q for F, caso contrário, será sempre V. Uma proposição r formada a partir de outras proposições é uma tautologia se r tiver sempre o valor lógico V independentemente dos valores lógicos das proposições que a formam. A partir dessas informações, julgue os itens que se seguem.
A negação da proposição "No estado democrático, não há soberano e ninguém exercerá o poder de forma ilimitada" é a proposição "No estado democrático, há um soberano e ninguém exercerá o poder de forma ilimitada".
- C. Certo
- E. Errado
Uma pesquisa envolvendo 85 juízes de diversos tribunais revelou que 40 possuíam o título de doutor, 50 possuíam o título de mestre, 20 possuíam somente o título de mestre e não eram professores universitários, 10 possuíam os títulos de doutor e mestre e eram professores universitários, 15 possuíam somente o título de doutor e não eram professores universitários e 10 possuíam os títulos de mestre e doutor e não eram professores universitários. Com base nessas informações, julgue os itens seguintes.
Mais de 3 desses juízes possuem somente o título de doutor e são professores universitários.
- C. Certo
- E. Errado
Raciocínio lógico - Proposição/Argumento - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2008
Uma proposição é uma oração declarativa — não é exclamativa nem interrogativa — que pode ser julgada como verdadeira (V) ou falsa (F). As proposições são representadas por letras p, q, r, s etc. Dada uma proposição p, a negação de p, indicada por ¬p, tem sempre o valor oposto ao de p. A partir de proposições dadas, pode-se construir novas proposições mediante o emprego de conectivos: o conectivo  colocado entre as proposições p e q dá origem à proposição p
colocado entre as proposições p e q dá origem à proposição p q (lê-se: p e q), que é V somente se ambas as proposições forem V, caso contrário, será F; o conectivo
q (lê-se: p e q), que é V somente se ambas as proposições forem V, caso contrário, será F; o conectivo 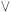 colocado entre as proposições p e q origina a proposição p
colocado entre as proposições p e q origina a proposição p q (lê-se: p ou q), que é F somente se ambas as proposições forem F, caso contrário, será V; e o conectivo → colocado entre as proposições p e q forma a proposição p → q (lê-se: se p então q), que é F somente se p for V e q for F, caso contrário, será sempre V. Uma proposição r formada a partir de outras proposições é uma tautologia se r tiver sempre o valor lógico V independentemente dos valores lógicos das proposições que a formam. A partir dessas informações, julgue os itens que se seguem.
q (lê-se: p ou q), que é F somente se ambas as proposições forem F, caso contrário, será V; e o conectivo → colocado entre as proposições p e q forma a proposição p → q (lê-se: se p então q), que é F somente se p for V e q for F, caso contrário, será sempre V. Uma proposição r formada a partir de outras proposições é uma tautologia se r tiver sempre o valor lógico V independentemente dos valores lógicos das proposições que a formam. A partir dessas informações, julgue os itens que se seguem.
A frase "No ano de 2007, o índice de criminalidade da cidade caiu pela metade em relação ao ano de 2006" é uma sentença aberta.
- C. Certo
- E. Errado
Uma pesquisa envolvendo 85 juízes de diversos tribunais revelou que 40 possuíam o título de doutor, 50 possuíam o título de mestre, 20 possuíam somente o título de mestre e não eram professores universitários, 10 possuíam os títulos de doutor e mestre e eram professores universitários, 15 possuíam somente o título de doutor e não eram professores universitários e 10 possuíam os títulos de mestre e doutor e não eram professores universitários. Com base nessas informações, julgue os itens seguintes.
Menos de 50 desses juízes possuem o título de doutor ou de mestre mas não são professores universitários.
- C. Certo
- E. Errado
Cinco moças, Ana, Beatriz, Carolina, Denise e Eduarda, estão vestindo blusas vermelhas ou amarelas. Sabe-se que as moças que vestem blusas vermelhas sempre contam a verdade e as que vestem blusas amarelas sempre mentem. Ana diz que Beatriz veste blusa vermelha. Beatriz diz que Carolina veste blusa amarela. Carolina, por sua vez, diz que Denise veste blusa amarela. Por fi m, Denise diz que Beatriz e Eduarda vestem blusas de cores diferentes. Por fi m, Eduarda diz que Ana veste blusa vermelha. Desse modo, as cores das blusas de Ana, Beatriz, Carolina, Denise e Eduarda são, respectivamente:
- A.
amarela, amarela, vermelha, vermelha e amarela.
- B.
vermelha, vermelha, vermelha, amarela e amarela.
- C.
vermelha, amarela, amarela, amarela e amarela.
- D.
vermelha, amarela, vermelha, amarela e amarela.
- E.
amarela, amarela, vermelha, amarela e amarela.
Raciocínio lógico - Proposição/Argumento - Centro de Seleção e de Promoção de Eventos UnB (CESPE) - 2008
Uma proposição é uma oração declarativa — não é exclamativa nem interrogativa — que pode ser julgada como verdadeira (V) ou falsa (F). As proposições são representadas por letras p, q, r, s etc. Dada uma proposição p, a negação de p, indicada por ¬p, tem sempre o valor oposto ao de p. A partir de proposições dadas, pode-se construir novas proposições mediante o emprego de conectivos: o conectivo  colocado entre as proposições p e q dá origem à proposição p
colocado entre as proposições p e q dá origem à proposição p q (lê-se: p e q), que é V somente se ambas as proposições forem V, caso contrário, será F; o conectivo
q (lê-se: p e q), que é V somente se ambas as proposições forem V, caso contrário, será F; o conectivo  colocado entre as proposições p e q origina a proposição p
colocado entre as proposições p e q origina a proposição p q (lê-se: p ou q), que é F somente se ambas as proposições forem F, caso contrário, será V; e o conectivo → colocado entre as proposições p e q forma a proposição p → q (lê-se: se p então q), que é F somente se p for V e q for F, caso contrário, será sempre V. Uma proposição r formada a partir de outras proposições é uma tautologia se r tiver sempre o valor lógico V independentemente dos valores lógicos das proposições que a formam. A partir dessas informações, julgue os itens que se seguem.
q (lê-se: p ou q), que é F somente se ambas as proposições forem F, caso contrário, será V; e o conectivo → colocado entre as proposições p e q forma a proposição p → q (lê-se: se p então q), que é F somente se p for V e q for F, caso contrário, será sempre V. Uma proposição r formada a partir de outras proposições é uma tautologia se r tiver sempre o valor lógico V independentemente dos valores lógicos das proposições que a formam. A partir dessas informações, julgue os itens que se seguem.
A frase "O triplo de quatro é menor do que dez?" é uma proposição falsa.
- C. Certo
- E. Errado


