Questões de Engenharia Cartográfica e de Agrimensura da Fundação Carlos Chagas (FCC)

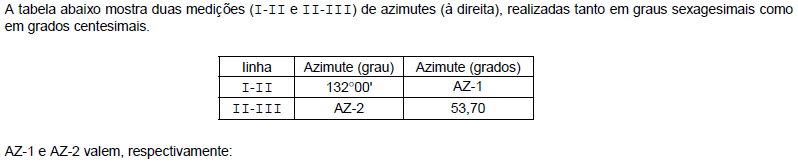
• A.

  155,33 e 44°22'

• B.

  150,00 e 46°30'

• C.

  149,50 e 49°30'

• D.

  123,45 e 43°21'

• E.

  146,67 e 48°20'

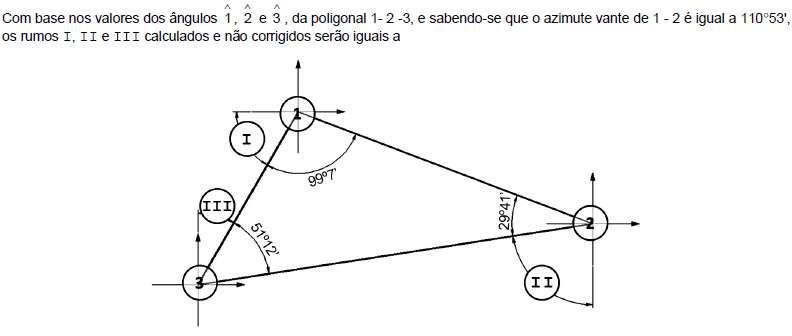
• A.

  59°10’; 58°20’; 57°30’.

• B.

  20°53’; 69°07’; 08°48’.

• C.

  20°53’; 81°12’; 30°00’.

• D.

  45°00’; 90°00’; 15°00’.

• E.

  60°00’; 81°12’; 30°00’.

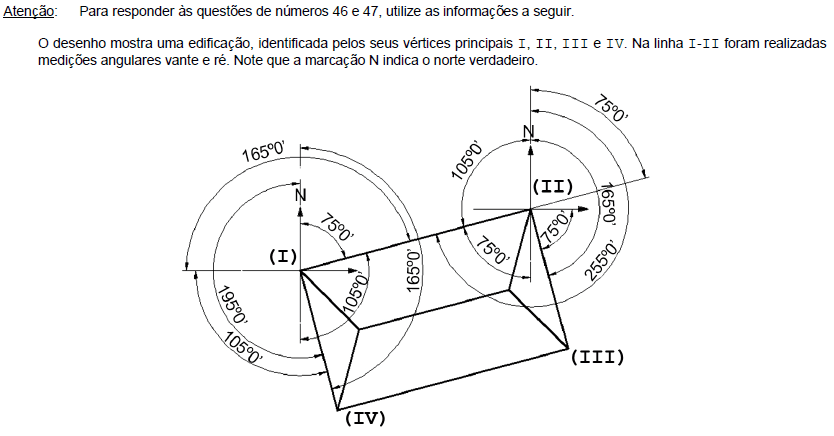
Os valores de rumo e o azimute vante da linha I-II são, respectivamente,

• A.

  75°00’ NE e 75°00’

• B.

  105°00 ’SE e 105°00’ SE

• C.

  75°00’ N e 105°00’ S

• D.

  165°00’ WE e 75°00’ NE

• E.

  165°00’ WE e 75°00’

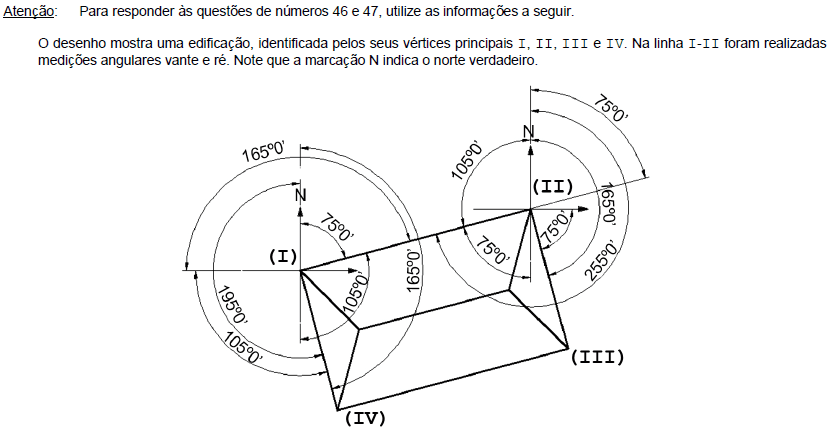
Os rumos vante e ré, assim como os azimutes vante e ré, da linha I-II são, respectivamente,

• A.

  105°00’ SE e 105°00’ NW; 105°00’ S e 105°00’ N

• B.

  75°00’ NE e 75°00’ SW; 75°00’ e 255°00’

• C.

  75°00’ NE e 105°00’ NW; 75°00’ S e 255°00’ N

• D.

  105°00’ SE e 75°00’ SW; 105°00’ SE e 255°00’ NW

• E.

  165°00’ WE e 75°00’ SW; 165°00’ WE e 105°00’ NW

Sobre as coordenadas cartesianas e arbitrárias,

• A.

  para que um sistema cartesiano seja anti-horário o eixo Z deve girar negativamente em relação ao eixo X.

• B.

  conforme a posição da direção positiva dos eixos, um sistema cartesiano pode ser dextro ou anti-dextro.

• C.

  um sistema de coordenadas cartesianas é caracterizado por um conjunto de três retas (X, Y, Z) triortonormais.

• D.

  um sistema cartesiano pode ser, ao mesmo tempo, levógiro e dextrógiro, dependendo da relação entre os eixos.

• E.

  um sistema dextrógiro é aquele em que um observador situado no plano XY vê o plano XZ cruzar o eixo YZ no semieixo esquerdo ao eixo Z.

Sobre a identificação de superfícies de referência, considere:

I. Na Agrimensura e Topografia, utilizam-se o modelo adotado pela Geodésia, o elipsoide de revolução ou biaxial que é a figura geométrica gerada pela rotação de uma semielipse (geratriz) em torno de um de seus eixos (eixo de revolução).

II. Em Geodésia, é tradicional considerar como parâmetros o semieixo maior a e o achatamento f, expresso pela equação f = (a−b)/a.

III. Outro modelo adotado pela Agrimensura e Topografia é o Geoide de Rupert ou Modelo Reverso de Mercator.

Está correto o que consta em

• A.

  II, apenas.

• B.

  I, II e III.

• C.

  I, apenas.

• D.

  I e III, apenas.

• E.

  I e II, apenas.

Sobre a identificação de superfícies de referência,

• A.

  o modelo geoidal é o que mais se aproxima da forma da Terra. É definido teoricamente como sendo o nível médio dos mares em repouso, prolongado através dos continentes.

• B.

  o modelo geoidal é uma superfície regular, de tratamento matemático simples, porém, com inúmeros dados a serem calculados, o que exige grande capacidade computacional.

• C.

  o geoide pode ser calculado pelas superfícies equipotenciais de cada quadrante do campo da gravidade ou superfície de nível regional.

• D.

  as altitudes ortométricas médias do geoide devem ser calculadas a partir do campo de gravidade médio da Terra, referenciados pelos polos verdadeiros e os referênciais físicos de Mercator.

• E.

  entende-se como um geoide de revolução a superfície formada pelos diferentes elipsoides de revolução referenciados na Terra, ajustados pelo campo gravitacional local.

A respeito da identificação de superfícies de referência,

• A.

  em trabalhos topográficos aplicados a obras ferroviárias pode-se adotar um modelo plano de referência desde que, na prática, a maior dimensão do retângulo limítrofe fique abaixo de 30 km.

• B.

  a superfície de projeção é um plano da superfície terrestre, considerando como origem do levantamento seu ponto mais SW, cujo referencial altimétrico é o datum superficial brasileiro.

• C.

  o plano de projeção tem a sua dimensão máxima limitada a 100 km, a partir da origem, limitando a desconsideração da curvatura terrestre a 1:350000 da maior dimensão vertical.

• D.

  o eixo das coordenadas do plano referencial é a horizontal azimutal, que dever ser, necessariamente, orientado para o norte geográfico.

• E.

  o plano nacional de referência (PNR) é, na verdade, um conjunto de planos que descrevem o território brasileiro, conforme a localidade, por levar em consideração a maior exatidão das verticalidades.

Sobre os tipos de nivelamento e suas características, analise:

I. Nivelamento que realiza a medida da diferença de nível entre pontos no terreno por intermédio de leituras correspondentes a visadas horizontais, obtidas com um nível, em miras colocadas verticalmente nos referidos pontos.

II. Nivelamento que realiza a medição da diferença de nível entre pontos no terreno, indiretamente, a partir da determinação do ângulo vertical da direção que os une e da distância entre estes, fundamentando-se na relação trigonométrica entre o ângulo e a distância medidos, levando em consideração a altura do centro do limbo vertical do teodolito ao terreno e a altura sobre o terreno do sinal visado.

III. Nivelamento trigonométrico em que as distâncias são obtidas taqueometricamente e a altura do sinal visado é obtida pela visada do fio médio do retículo da luneta do teodolito sobre uma mira colocada, verticalmente, no ponto cuja diferença de nível, em relação à estação do teodolito, é objeto de determinação.

As descrições dos itens I, II, e III estão relacionadas, respectivamente, aos tipos de nivelamentos:

• A.

  Geométrico; Geométrico; Taqueométrico.

• B.

  Geométrico; Trigonométrico; Taqueométrico.

• C.

  Taqueométrico; Trigonométrico; Geométrico.

• D.

  Trigonométrico; Taqueométrico; Geométrico.

• E.

  Taqueométrico; Taqueométrico; Trigonométrico.

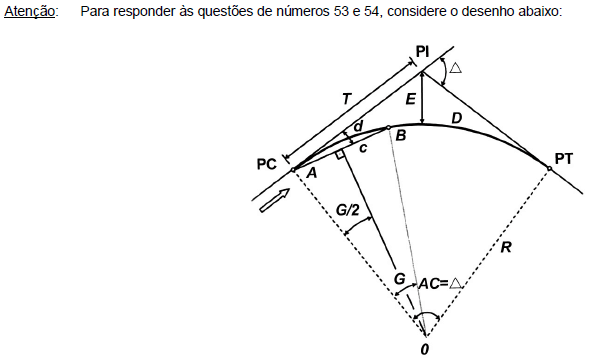
• A.

  Grau da Curva, Locação, Afastamento, Visada, Ângulo Interno.

• B.

  Abertura, Contra-Raio, Ângulo Interno, Visada, Corda Externa.

• C.

  Grau da Curva, Tiro, Afastamento, Visada, Ângulo interno.

• D.

  Ângulo de Deflexão, Contra-Raio, Visada, Afastamento, Tiro.

• E.

  Ângulo de Deflexão, Afastamento, Deflexão sobre a Tangente, Grau da Curva, Tangente Externa.