Questões de Estatística

Um analista deseja inspecionar um lote de 500 pacotes com encomendas internacionais. Como essa inspeção requer a abertura de cada pacote, ele decidiu fazê-la por amostragem, selecionando n pacotes desse lote. O analista dispõe de um cadastro que permite localizar precisamente cada pacote do lote por meio de um código de identificação.

Com base nessas informações e nos conceitos de amostragem, julgue os itens a seguir.

Na estimação de uma proporção p por amostragem aleatória simples, a variância do estimador é máxima quando p = 0,5.

• C. Certo
• E. Errado

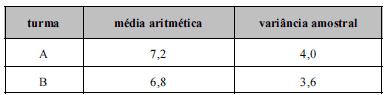
Um estudo foi realizado em determinada escola para se avaliar o efeito, no desempenho dos estudantes, do uso de computadores em sala de aula. Para esse estudo, foram selecionados aleatoriamente 60 alunos de determinado ano escolar, separando-os em duas turmas A e B, cada uma com 30 alunos. Ao longo de um semestre letivo, um método de ensino com auxílio de computadores foi aplicado na turma A, enquanto, nesse mesmo período, outro método sem auxílio de computadores foi aplicado na turma B. Ao final desse semestre, o mesmo teste foi aplicado para os 60 alunos participantes desse estudo. O quadro acima mostra algumas estatísticas acerca das notas obtidas pelos alunos de ambas as turmas.

Considerando essas informações, acerca de probabilidade, inferência e amostragem, julgue os itens a seguir.

• C. Certo
• E. Errado

Em uma regressão logística, considere a variável resposta (Y) como óbito de recém-nascidos (1 indica morte, 0 indica não morte) e a variável explicativa (X) sendo peso ao nascer, em quilos. O resultado do cálculo de E(Y) quando X vale 1,0 é 0,7. Esse 0,7 é a probabilidade de o recém-nascido

• A.

  viver, quando seu peso no nascimento é um quilo.

• B.

  falecer, quando seu peso no nascimento é um quilo.

• C.

  ter nascido com um quilo, dado que ele viveu.

• D.

  ter nascido com um quilo, dado que ele faleceu.

• E.

  ter nascido com um quilo, independentemente de viver ou falecer.

Considerando as densidades de probabilidade ilustradas na figura acima, julgue os itens que se seguem a respeito dos momentos dessas distribuições.

Se a distribuição A for gama, com parâmetros 1,5 e 1,0, então a média e a moda dessa distribuição serão iguais.

• C. Certo
• E. Errado

Um analista deseja inspecionar um lote de 500 pacotes com encomendas internacionais. Como essa inspeção requer a abertura de cada pacote, ele decidiu fazê-la por amostragem, selecionando n pacotes desse lote. O analista dispõe de um cadastro que permite localizar precisamente cada pacote do lote por meio de um código de identificação.

Com base nessas informações e nos conceitos de amostragem, julgue os itens a seguir.

Se o analista desejar fazer uma amostragem intencional (não probabilística) de tamanho n = 10, com base em sua experiência pessoal, então, nesse caso, a variância do estimador de uma proporção p será igual a u(1 - u)/500, em que u é uma probabilidade a priori estabelecida subjetivamente pelo analista.

• C. Certo
• E. Errado

Os aposentos de um hotel internacional estão distribuídos em corredores com uma dúzia de apartamentos de cada lado. Um dos corredores está com os apartamentos ocupados, exceto um deles, que fica no meio do corredor. Um hóspede chega ao hotel e será acomodado naquele aposento. Se os hóspedes já acomodados naquele corredor forem redistribuídos aleatoriamente no mesmo corredor, e, exatamente, dez deles tiverem a mesma nacionalidade do hóspede que será acomodado agora, então a probabilidade de que os três vizinhos — à esquerda, à direita e à frente — do novo hóspede sejam seus compatriotas é

• A.

  menor que 5%.

• B.

  maior que 5%, mas menor que 10%.

• C.

  maior que 10%, mas menor que 15%.

• D.

  maior que 15%, mas menor que 20%.

• E.

  maior que 20%.

Considere que a chegada e o atendimento de estudantes em determinada fila para matrícula em uma escola possam ser modelados segundo um passeio aleatório simples em tempo discreto t = 0, 1, 2, 3 ... e que, em cada instante t, apenas dois eventos sejam possíveis: ou um novo estudante entra na fila com probabilidade p ou um estudante na fila é atendido com probabilidade 1 - p. Suponha, ainda, que, no instante inicial t = 0, a quantidade de estudantes na fila não seja nula e grande o suficiente para que a fila não fique vazia em pouco tempo, e que, a cada instante t, no máximo um estudante pode ser atendido.

Com base nessa situação, julgue os itens a seguir.

Na situação em que se consideram apenas os dois instantes iniciais, sendo t = 1 e t = 2, e p = 0,6, é mais provável que a fila não cresça.

• C. Certo
• E. Errado

Em um modelo de regressão logística, o que indica se o modelo se ajusta bem aos dados é a(o)

• A.

  função logito

• B.

  função probito

• C.

  razão de chances

• D.

  estatística deviance

• E.

  coeficiente de determinação

Um analista deseja inspecionar um lote de 500 pacotes com encomendas internacionais. Como essa inspeção requer a abertura de cada pacote, ele decidiu fazê-la por amostragem, selecionando n pacotes desse lote. O analista dispõe de um cadastro que permite localizar precisamente cada pacote do lote por meio de um código de identificação.

Com base nessas informações e nos conceitos de amostragem, julgue os itens a seguir.

A disponibilidade do cadastro permite que o analista efetue uma seleção por amostragem aleatória simples ou por amostragem sistemática com base nos códigos de identificação dos pacotes.

• C. Certo
• E. Errado

Dado um conjunto finito ��, chamamos de conjunto das partes de ��ou 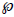��) ao conjunto cujos elementos são todos os subconjuntos de ��. Com base nesta definição, é CORRETO afirmar que

• A.

  ∅é elemento de  �� , se, e somente se for elemento também de ��.

• B.

  ∅é elemento de  �� , qualquer que seja o conjunto ��.

• C.

  {∅}é elemento de ��, ) se, e somente se, for elemento também do conjunto ��.

• D.

  {∅}jamais pode ser elemento de  �� , pois �� é assumido como conjunto finito.

• E.

  Se �� ≠ ∅, então {∅} é elemento de (��)