Questões de Estatística

Para uma pesquisa piloto, realizada em uma grande cidade, escolheu-se aleatoriamente 300 habitantes e 75% deles estavam favoráveis à construção de uma ponte. Considere que é normal a distribuição amostral da frequência relativa dos habitantes favoráveis à construção da ponte e que na curva normal padrão (Z) têm-se as probabilidades P(Z > 1,96) = 0,025 e P(Z > 1,64) = 0,05. A amplitude do intervalo de confiança para a proporção correspondente à pesquisa, ao nível de 95%, é, em porcentagem, igual a

• A. 7,4.
• B. 7,0.
• C. 8,2.
• D. 9,8.
• E. 9,0.

• A. [8,945 ; 11,055].
• B. [8,940 ; 11,060].
• C. [8,935 ; 11,065].
• D. [8,930 ; 11,070].
• E. [8,950 ; 11,050].

Em um determinado ramo de atividade, a população de todos os salários dos empregados é considerada normal e de tamanho infinito. O desvio padrão populacional apresenta um valor igual a R$ 200,00. Deseja-se testar a hipótese H₀: = μ = R$ 1.700,00 (hipótese nula) contra H₁: μ ≠ R$ 1.700,00 (hipótese alternativa) com base em uma amostra aleatória de tamanho 64 extraída da população (μ é a média da população). A média encontrada para esta amostra apresentou um valor igual a M reais. Fixando o nível de significância do teste em 5% e considerando que na curva normal padrão (Z) as probabilidades P(Z > 1,96) = 0,025 e P(Z > 1,64) = 0,05, H0 não será rejeitada caso

• A. 1.387,50 < M ¡Ü 1.477,50.
• B. 1.477,50 < M ¡Ü 1.567,50.
• C. 1.567,50 < M ¡Ü 1.657,50.
• D. 1.657,50 < M ¡Ü 1.747,50.
• E. 1.747,50 < M ¡Ü 1.835,50.

De uma população com 1.025 elementos, considerada normalmente distribuída, é extraída uma amostra aleatória, com reposição, de tamanho 400 obtendo-se uma média amostral igual a 156. Sendo μ a média da população, deseja-se testar a hipótese H₀: μ = 150 (hipótese nula) contra H₁: μ > 150 (hipótese alternativa), ao nível de significância α, com base nos dados da amostra. Considere que na curva normal padrão (Z) a probabilidade P(Z > 2,40) = α e que o valor encontrado para a média amostral coincide com o maior valor tal que H₀ não é rejeitada ao nível de significância α. O desvio padrão populacional é igual a

• A. 125.
• B. 100.
• C. 64.
• D. 200.
• E. 144.

Dois grupos são formados, respectivamente, de amostras aleatórias independentes provenientes de duas populações constituídas de escores. Pretende-se aplicar o teste da mediana, cujo objetivo é verificar se as medianas dos grupos são iguais. Sobre este teste, considere as seguintes afirmações: I. Não poderá ser aplicado caso sejam desconhecidas as distribuições das populações dos grupos. II. Poderá ser aplicado mesmo que os tamanhos dos grupos sejam diferentes. III. Não poderá ser aplicado caso ocorra, pelo menos, um empate entre os dados dos dois grupos. IV. Poderá ser aplicado se combinando os escores dos dois grupos, verifica-se que o valor da mediana do conjunto formado não pertence a qualquer um dos grupos. Está correto o que consta APENAS em

• A. I e II.
• B. II e IV.
• C. I e III.
• D. III e IV.
• E. II, III e IV.

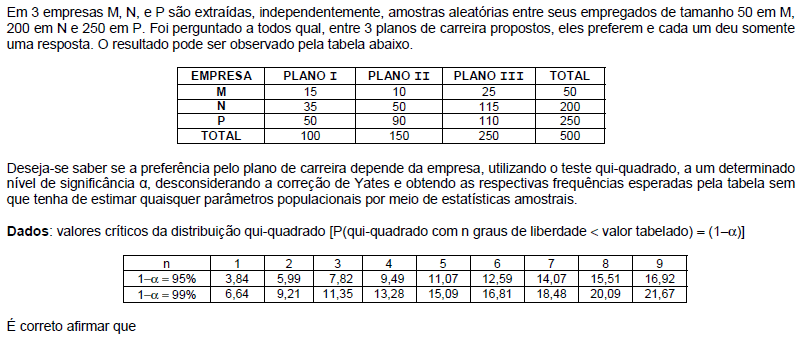
• A. para qualquer nível de significância superior a 1% a conclusão é que a preferência depende da empresa.
• B. o valor do qui-quadrado observado é inferior a 12.
• C. tanto ao nível de significância de 1% como ao nível de significância de 5%, a conclusão é que a preferência independe da empresa.
• D. não existe um nível de significância inferior a 1% tal que a conclusão é que a preferência independe da empresa.
• E. o número de graus de liberdade do teste é igual a 8.

• A.
• B.
• C.
• D.
• E.

• A. 12,0.
• B. 15,0.
• C. 16,0.
• D. 14,5.
• E. 17,5.

Seja o modelo linear Y_i = α + βX_i + γD_i + ε_i, em que Y_i representa o salário mensal do empregado i em uma grande empresa, X_i o tempo de experiência em anos de i, D_i = 0 se i não possuir curso superior e D_i = 1 se i possuir curso superior. α, β e γ são parâmetros desconhecidos e εi é o erro aleatório com as respectivas hipóteses da correspondente regressão. As estimativas de α, β e γ foram obtidas pelo método dos mínimos quadrados e todas apresentaram valores maiores que zero. Com relação a este modelo, a função de salário mensal de um empregado com curso superior

• A. apresenta um intercepto igual ao intercepto da função de salário mensal de um empregado sem curso superior.
• B. apresenta um intercepto igual a (α + β).
• C. apresenta uma inclinação, em relação aos anos de experiência, igual à função de salário mensal de um empregado sem curso superior.
• D. indica que se um empregado com nível superior tiver o mesmo tempo de experiência que um empregado sem nível superior, ele ganhará a mais o valor (α + γ).
• E. indica que é impossível que o salário de um empregado sem nível superior seja igual ao salário de um empregado com nível superior.

Em 10 grandes empresas foram escolhidos aleatoriamente em cada uma 5 empregados para realizar uma determinada tarefa, independentemente, sendo anotado o tempo em horas que cada empregado demorou para realizar a tarefa. Deseja-se saber, a um determinado nível de significância, se os tempos médios das empresas para a realização da tarefa são iguais. Pelo quadro de análise de variância, a soma de quadrados, devido à fonte de variação total, é igual a 1.400 e o valor da estatística F (F calculado), utilizado para testar a igualdade dos tempos médios entre as empresas, apresentou um valor igual a 15. Neste quadro, o correspondente valor da soma de quadrados entre empresas é igual a

• A. 720.
• B. 900.
• C. 1.200.
• D. 1.080.
• E. 820.