Questões de Estatística do ano 2004
Lista completa de Questões de Estatística do ano 2004 para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.

Considerando a situação descrita acima, julgue os itens subseqüentes.
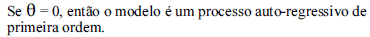
- C. Certo
- E. Errado

Considerando a situação descrita acima, julgue os itens subseqüentes.
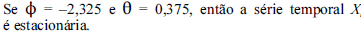
- C. Certo
- E. Errado

Considerando a situação descrita acima, julgue os itens subseqüentes.

- C. Certo
- E. Errado

Considerando a situação descrita acima, julgue os itens subseqüentes.
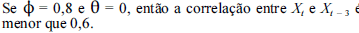
- C. Certo
- E. Errado

Considerando a situação descrita acima, julgue os itens subseqüentes.

- C. Certo
- E. Errado
O teste aleatorizado uniformemente mais potente para o problema de testar a hipótese
H : λ ≤ 0,03contra a alternativa A : λ > 0,03, com tamanho α = 0,05 , para uma amostra aleatória X1,...;X20 da distribuição de Poisson com parâmetro λ tem a forma

onde as constantes
c e k devem satisfazer a condição =0,05 quando λ = 0, 03.
=0,05 quando λ = 0, 03. Sabe-se que se Y tem distribuição de Poisson com parâmetro 0,6 então
P(Y=0)=0,5488, P(Y=1)=0,3293e P(Y=2)=0,0988. Assinale a opção que dá os valores das constantes
c e k <FONT face- A.
c=0,300;k=1
- B.
c=0, 400;k=2
- C.
c=0,300;k=2
- D.
c=0, 272;k=1
- E.
c=0, 272;k=2
Estatística - Teste de Hipótese - Fundação de Estudos Superiores de administração e Gerência (ESAG) - 2004
Em uma pesquisa prévia eleitoral três candidatos conseguiram os seguintes percentuais de intenção de voto, para uma amostra de 400 eleitores:
Utilizando-se intervalos de confiança de 95% de probabilidade pode-se afirmar que:
- A.
o candidato "A" seria o vencedor se a eleição fosse realizada no período da pesquisa.
- B.
os resultados apontam um empate técnico entre os candidatos "A" e "B" para o primeiro lugar, e também empate técnico entre os candidatos "B" e "C" para o segundo lugar.
- C.
o candidato "A" seria o primeiro colocado, mas haveria uma indefinição para o segundo lugar entre os demais candidatos.
- D.
para primeiro lugar, existe empate técnico entre os candidatos "A" e "B".
Estatística - Teste de Hipótese - Fundação de Estudos Superiores de administração e Gerência (ESAG) - 2004
O tempo de montagem de um equipamento apresenta uma distribuição normal com média igual a 30 minutos e desvio padrão igual a 5 minutos.
Novas linhas de produção foram idealizadas para reduzir o tempo de montagem.
A montagem de 36 novos equipamentos em cada uma das duas novas
linhas de produção apresenta os seguintes resultados:
Através dos Testes Unilaterais de Médias, com nível de significância de 2,5%, constata-se que:
- A.
a linha 1 tende a aumentar o tempo de montagem.
- B.
as duas novas linhas de produção tendem a reduzir o tempo de montagem.
- C.
nenhuma das duas linhas tendem a reduzir o tempo de montagem.
- D.
apenas a linha 2 tende a reduzir o tempo de montagem.
Estatística - Teste de Hipótese - Fundação de Estudos Superiores de administração e Gerência (ESAG) - 2004
Uma linha de produção apresenta 15% de itens defeituosos. Após a aquisição de novas máquinas, uma amostra de 300 peças revelou que 27 eram defeituosas. Por meio de um teste unilateral de proporções, com nível de significância de 5%, chega-se à seguinte conclusão:
- A.
Houve melhoria na qualidade da peças produzidas com a aquisição das novas máquinas.
- B.
O tamanho da amostra é inadequado para realização do teste de hipótese.
- C.
Houve uma redução na qualidade das peças produzidas
- D.
Não houve modificação na qualidade das peças produzidas
Para os itens a seguir, utilize, se necessário, as tabelas abaixo para calcular os valores das probabilidades da distribuição normal padrão e valores de
Uma unidade de produção demanda uma quantidade aleatória D (em kg/dia) de um componente químico. A unidade de produção mantém um estoque X desse componente em kg/dia. Sabe-se que as duas variáveis aleatórias são normais. A distribuição conjunta (D, X) está representada pela tabela abaixo.
Com base na situação hipotética acima, julgue os itens a seguir.
A diferença entre o estoque e a demanda é, em média, igual a 2 kg/dia.
- C. Certo
- E. Errado


