Questões de Estatística do ano 2005

Um fabricante afirma que pelo menos 95% dos equipamentos que fornece à indústria encontram-se dentro de suas especificações. Uma amostra de 200 itens escolhidos ao acaso revelou 10 itens fora de especificação. Assinale a opção que corresponde ao valor probabilístico (pvalor) do teste de H:θ ≥0,95contra A:θ <0,95, sendo θ a proporção populacional de itens dentro de especificação.

• a.

  0,500

• b.

  0,050

• c.

  0,025

• d.

  0,010

• e.

  0,100

Uma empresa verificou que, historicamente, a idade média dos consumidores de seu principal produto é de 25 anos, considerada baixa por seus dirigentes. Com o objetivo de ampliar sua participação no mercado, a empresa realizou uma campanha de divulgação voltada para consumidores com idades mais avançadas. Um levantamento realizado para medir o impacto da campanha indicou que as idades dos consumidores apresentaram a seguinte distribuição:

Assinale a opção que corresponde ao resultado da campanha considerando o seguinte critério de decisão: se a diferença  for maior que o valor ,  então a campanha de divulgação surtiu efeito, isto é, a idade média aumentou; caso contrário, a campanha de divulgação não alcançou o resultado desejado.

• A. A campanha surtiu efeito, pois , é maior que
• B. A campanha não surtiu efeito, pois é menor que
• C. A campanha surtiu efeito, pois é maior que
• D. A campanha não surtiu efeito, pois  é menor que
• E. A campanha surtiu efeito, pois é maior que

Lança-se uma moeda 20 vezes e observa-se a ocorrência de 7 caras. Seja θ a probabilidade de cara. Assinale a opção que dá o valor da estatística teste correspondente ao teste da hipótese H:θ ≥0,5 contra a alternativa A:θ <0,5.

• A.
• B.
• C.
• D.
• E.

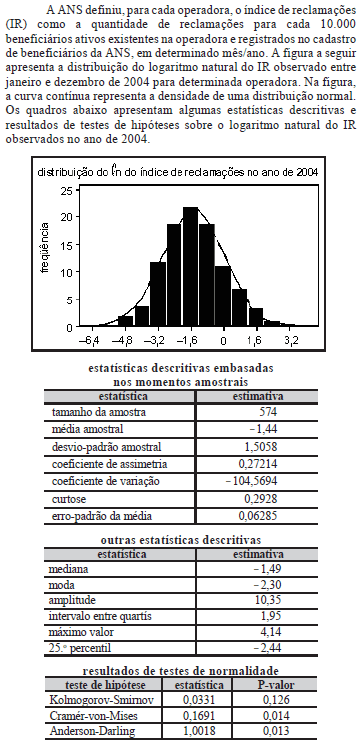
Com relação às informações apresentadas no texto acima, julgue os seguintes itens.

O resultado do teste de Kolmogorov-Smirnov permite inferir que a distribuição do logaritmo natural do IR na situação descrita é normal, se for considerado um nível de significância igual a 5%.

• C. Certo
• E. Errado

Com relação às informações apresentadas no texto acima, julgue os seguintes itens.

No presente caso, o resultado do teste de Cramér-von- Mises permite inferir que a distribuição do logaritmo natural do IR é normal, se for considerado um nível de significância igual a 2%.

• C. Certo
• E. Errado

Com relação às informações apresentadas no texto acima, julgue os seguintes itens.

O resultado do teste de Anderson-Darling permite inferir que a distribuição do logaritmo natural do IR na situação descrita é normal, se o nível de significância considerado for igual a 1%.

• C. Certo
• E. Errado

A partir das informações do texto acima, julgue os itens que se sucedem.

A variância amostral dos preços cobrados para a movimentação de contêineres apenas nos portos de Santos e de Paranaguá é inferior a R$ 7.500,00.

• C. Certo
• E. Errado

Uma pesquisa coletou dados acerca dos salários do mês de julho de 2004 de 400 empregados que ocupavam o cargo de auxiliar administrativo, do tempo de experiência no cargo e do sexo de cada entrevistado. A amostra foi aleatória simples. Os empregados participantes da pesquisa foram sorteados a partir de um cadastro muito grande fornecido por uma associação de trabalhadores. A pesquisa constatou que 40% dos pesquisados eram do sexo masculino e a parcela restante era do sexo feminino. A média amostral dos salários das mulheres foi 50% maior que a média amostral dos salários dos homens. A margem de erro da pesquisa para a estimação do salário médio dos auxiliares administrativos foi de R$ 15,00, com 95% de confiança. As tabelas I e II apresentam os principais resultados dessa pesquisa. A tabela III apresenta alguns valores da distribuição normal padrão, segundo o nível de confiança.

 

Com base nas informações do texto e das tabelas acima, julgue os itens de 66 a 85.

Se as variâncias dos salários entre os homens e entre as mulheres forem iguais, então o coeficiente de variação dos salários dos homens será superior ao coeficiente de variação dos salários das mulheres.

• C. Certo
• E. Errado

No contexto das propriedades dos estimadores de mínimos quadrados, e considerando os seguintes pressupostos:

i) yt = β1 + β2xt + et

ii) E[ et ] = 0

iii) var ( et ) = σ2

iv)cov ( ei , e j ) = 0

v) xt ≠ c , para toda observação

é verdadeiro afirmar que:

• A.

  dada a observância dos pressupostos ( i ) a ( v ), os estimadores de mínimos quadrados de β1 e β2 possuem variância mínima entre todos os estimadores lineares e não-lineares.

• B.

  a hipótese ( iii ) expressa a condição de não existência de correlação serial dos resíduos.

• C.

  a hipótese ( iv ) expressa a condição requerida de homoscedasticidade.

• D.

  a validade do teorema de Gauss-Markov não depende da hipótese de normalidade do erro ( et ).

Os dados a seguir referem-se às questões de números 38 e 39.

A variância das notas vale, aproximadamente:

• A.

  0,5

• B.

  0,75

• C.

  0,81

• D.

  1

• E.

  1,13